


Next: Potential Due to a
Up: Gravitational Potential Theory
Previous: Roche Radius
Precession and Forced Nutation of the Earth
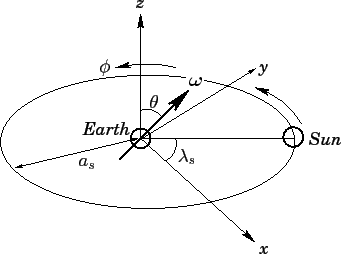
Consider the Earth-Sun system--see Figure 45. From a geocentric viewpoint, the Sun orbits the Earth counter-clockwise (looking from the north), once per year, in an approximately circular orbit
of radius
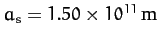 . In astronomy, the plane of the Sun's
apparent orbit relative to the Earth is known as the ecliptic plane.
Let us define non-rotating Cartesian coordinates, centered on the Earth, which are such that the
. In astronomy, the plane of the Sun's
apparent orbit relative to the Earth is known as the ecliptic plane.
Let us define non-rotating Cartesian coordinates, centered on the Earth, which are such that the 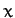 - and
- and 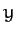 -axes lie in the
ecliptic plane, and the
-axes lie in the
ecliptic plane, and the 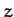 -axis is normal to this plane (in the
sense that the Earth's north pole lies at positive
-axis is normal to this plane (in the
sense that the Earth's north pole lies at positive 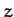 ). It follows that
the
). It follows that
the 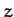 -axis is directed toward a point in the sky (located in the constellation Draco) known as the north
ecliptic pole. In the following, we shall treat the
-axis is directed toward a point in the sky (located in the constellation Draco) known as the north
ecliptic pole. In the following, we shall treat the 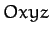 system as inertial. This is a reasonable
approximation because the orbital acceleration of the Earth is much smaller than the acceleration due to its diurnal rotation.
It is convenient to parameterize the instantaneous position
of the Sun in terms of a counter-clockwise (looking from the north) azimuthal angle
system as inertial. This is a reasonable
approximation because the orbital acceleration of the Earth is much smaller than the acceleration due to its diurnal rotation.
It is convenient to parameterize the instantaneous position
of the Sun in terms of a counter-clockwise (looking from the north) azimuthal angle 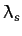 that is zero on the positive
that is zero on the positive 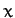 -axis--see Figure 45.
-axis--see Figure 45.
Figure 45:
The Earth-Sun system.
 |
Let
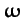 be the Earth's angular velocity vector due to its
daily rotation. This vector makes an angle
be the Earth's angular velocity vector due to its
daily rotation. This vector makes an angle  with the
with the 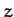 -axis,
where
-axis,
where
 is the mean inclination of the ecliptic to the
Earth's equatorial plane. Suppose that the projection of
is the mean inclination of the ecliptic to the
Earth's equatorial plane. Suppose that the projection of
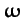 onto the ecliptic plane subtends an angle
onto the ecliptic plane subtends an angle 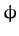 with the
with the 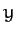 -axis,
where
-axis,
where 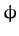 is measured in a counter-clockwise (looking from the north) sense--see Figure 45.
The orientation of the Earth's axis of rotation (which is, of course, parallel
to
is measured in a counter-clockwise (looking from the north) sense--see Figure 45.
The orientation of the Earth's axis of rotation (which is, of course, parallel
to
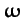 ) is thus determined by the two angles
) is thus determined by the two angles  and
and 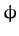 .
Note, however, that these two angles are also Euler angles, in
the sense given in Chapter 8. Let us examine the Earth-Sun
system at an instant in time,
.
Note, however, that these two angles are also Euler angles, in
the sense given in Chapter 8. Let us examine the Earth-Sun
system at an instant in time,  , when
, when  : i.e., when
: i.e., when
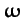 lies in the
lies in the 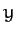 -
-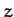 plane. At this particular instant, the
plane. At this particular instant, the 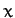 -axis points towards the so-called vernal equinox,
which is defined as the point in the sky where the ecliptic plane crosses the projection of the Earth's
equator (i.e., the plane normal to
-axis points towards the so-called vernal equinox,
which is defined as the point in the sky where the ecliptic plane crosses the projection of the Earth's
equator (i.e., the plane normal to
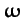 ) from south to north. A counter-clockwise (looking from the north) angle in the
ecliptic plane that is zero at the vernal equinox is generally known as an ecliptic longitude. Thus,
) from south to north. A counter-clockwise (looking from the north) angle in the
ecliptic plane that is zero at the vernal equinox is generally known as an ecliptic longitude. Thus, 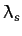 is the
Sun's ecliptic longitude.
is the
Sun's ecliptic longitude.
According to Equation (926), the potential energy of
the Earth-Sun system is written
![\begin{displaymath}
U = M_s\,\Phi = - \frac{G\,M_s\,M}{a_s} + \frac{G\,M_s\,(I_\parallel-I_\perp)}{a_s^{\,3}}\,P_2[\cos(\gamma_s)],
\end{displaymath}](img2271.png) |
(957) |
where  is the mass of the Sun,
is the mass of the Sun, 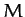 the mass of the Earth,
the mass of the Earth,
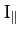 the Earth's moment of inertia about its axis of rotation,
the Earth's moment of inertia about its axis of rotation,
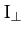 the Earth's moment of inertia about an axis lying in its
equatorial plane, and
the Earth's moment of inertia about an axis lying in its
equatorial plane, and
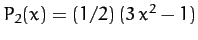 . Furthermore,
. Furthermore, 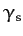 is the angle subtended
between
is the angle subtended
between
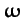 and
and 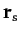 , where
, where 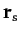 is the
position vector of the Sun relative to the Earth.
is the
position vector of the Sun relative to the Earth.
It is easily demonstrated that (with  )
)
 |
(958) |
and
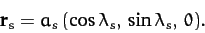 |
(959) |
Hence,
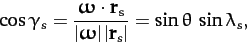 |
(960) |
giving
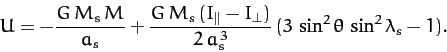 |
(961) |
Now, we are primarily interested in the motion of the Earth's axis of rotation over time-scales that are much
longer than a year, so we can average the above
expression over the Sun's orbit to give
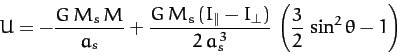 |
(962) |
(since the average of
 over a year is
over a year is 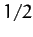 ).
Thus, we obtain
).
Thus, we obtain
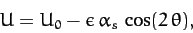 |
(963) |
where 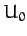 is a constant, and
is a constant, and
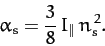 |
(964) |
Here,
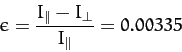 |
(965) |
is the Earth's ellipticity,
and
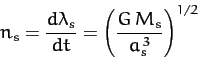 |
(966) |
the Sun's apparent orbital angular velocity.
According to Section 8.9, the rotational kinetic
energy of the Earth can be written
 |
(967) |
where the Earth's angular velocity
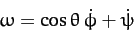 |
(968) |
is a constant of the motion.
Here, 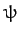 is the third Euler angle.
Hence, the Earth's Lagrangian takes the form
is the third Euler angle.
Hence, the Earth's Lagrangian takes the form
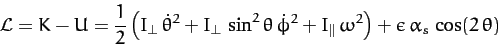 |
(969) |
where any constant terms have been neglected.
One equation of motion which can immediately be derived from this Lagrangian is
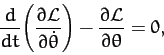 |
(970) |
which reduces to
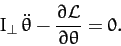 |
(971) |
Consider steady precession of the Earth's rotational axis, which is characterized by
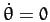 , with both
, with both 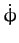 and
and  constant. It follows, from the above equation, that
such motion must satisfy the constraint
constant. It follows, from the above equation, that
such motion must satisfy the constraint
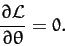 |
(972) |
Thus, we obtain
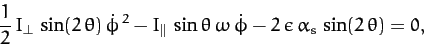 |
(973) |
where use has been made of Equations (968) and (969).
Now, as can easily be verified after the fact,
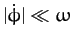 , so the above equation reduces to
, so the above equation reduces to
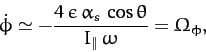 |
(974) |
which can be integrated to give
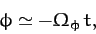 |
(975) |
where
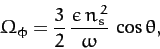 |
(976) |
and use has been made of Equation (964).
According to the above expression, the mutual interaction between the Sun and
the quadrupole gravitational field generated by the Earth's slight oblateness causes
the Earth's axis of rotation to precess steadily about the normal to the ecliptic
plane at the rate 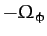 . The fact that
. The fact that 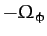 is
negative implies that the precession is in the opposite direction
to the direction of the Earth's rotation and the Sun's apparent orbit about the Earth. Incidentally, the interaction causes a precession
of the Earth's rotational axis, rather than the plane of the Sun's orbit,
because the Earth's axial moment of inertia is much less than
the Sun's orbital moment of inertia.
The precession period in years is given by
is
negative implies that the precession is in the opposite direction
to the direction of the Earth's rotation and the Sun's apparent orbit about the Earth. Incidentally, the interaction causes a precession
of the Earth's rotational axis, rather than the plane of the Sun's orbit,
because the Earth's axial moment of inertia is much less than
the Sun's orbital moment of inertia.
The precession period in years is given by
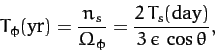 |
(977) |
where
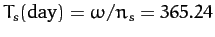 is
the Sun's orbital period in days. Thus, given that
is
the Sun's orbital period in days. Thus, given that
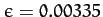 and
and
 , we obtain
, we obtain
 |
(978) |
Unfortunately, the observed precession period of the Earth's axis of rotation about the normal to the ecliptic plane is approximately 25,800 years, so something is clearly missing from
our model. It turns out that the missing factor is the influence of the Moon.
Using analogous arguments to those given above, the potential energy of the Earth-Moon system can be
written
![\begin{displaymath}
U = - \frac{G\,M_m\,M}{a_m} + \frac{G\,M_m\,(I_\parallel-I_\perp)}{a_m^{\,3}}\,P_2[\cos(\gamma_m)],
\end{displaymath}](img2302.png) |
(979) |
where  is the lunar mass, and
is the lunar mass, and 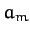 the radius of the Moon's (approximately circular) orbit. Furthermore,
the radius of the Moon's (approximately circular) orbit. Furthermore,  is the angle subtended
between
is the angle subtended
between
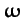 and
and 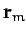 , where
, where
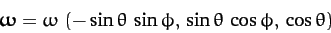 |
(980) |
is the Earth's angular velocity vector, and
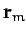 is the
position vector of the Moon relative to the Earth. Here, for the moment, we have retained the
is the
position vector of the Moon relative to the Earth. Here, for the moment, we have retained the 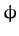 dependence in our expression for
dependence in our expression for
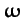 (since we shall presently differentiate by
(since we shall presently differentiate by 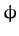 , before setting
, before setting  ). Now, the Moon's orbital plane
is actually slightly inclined to the ecliptic plane, the angle of inclination being
). Now, the Moon's orbital plane
is actually slightly inclined to the ecliptic plane, the angle of inclination being
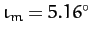 . Hence, we can write
. Hence, we can write
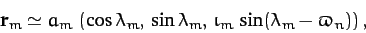 |
(981) |
to first order in  , where
, where 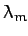 is the Moon's ecliptic longitude, and
is the Moon's ecliptic longitude, and 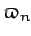 is the ecliptic longitude of the
lunar ascending node, which is defined as the point on the lunar orbit where the
Moon crosses the ecliptic plane from south to north. Of course,
is the ecliptic longitude of the
lunar ascending node, which is defined as the point on the lunar orbit where the
Moon crosses the ecliptic plane from south to north. Of course, 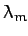 increases at the rate
increases at the rate 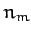 ,
where
,
where
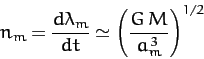 |
(982) |
is the Moon's orbital angular velocity. It turns out that the lunar ascending node precesses steadily,
in the opposite direction to the Moon's orbital rotation, in such a manner that it completes a
full circuit every 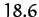 years. This precession is caused by the perturbing influence of the
Sun--see Chapter 14. It follows that
years. This precession is caused by the perturbing influence of the
Sun--see Chapter 14. It follows that
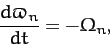 |
(983) |
where
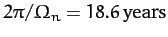 .
Now, from (980) and (981),
.
Now, from (980) and (981),
 |
(984) |
so (979) yields
to first order in  .
Given that we are interested in the motion of the Earth's axis of rotation on time-scales that are much longer than a month, we can average the above expression over the Moon's orbit to give
.
Given that we are interested in the motion of the Earth's axis of rotation on time-scales that are much longer than a month, we can average the above expression over the Moon's orbit to give
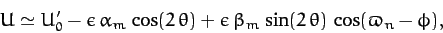 |
(986) |
[since the average of
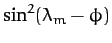 over a month is
over a month is 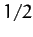 , whereas that of
, whereas that of
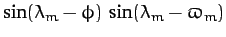 is
is
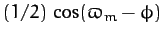 ]. Here,
]. Here, 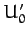 is a constant,
is a constant,
and
 |
(989) |
is the ratio of the lunar to the terrestrial mass.
Now, gravity is a superposable force, so the total potential energy of the Earth-Moon-Sun system is
the sum of Equations (963) and (986). In other words,
 |
(990) |
where 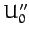 is a constant, and
is a constant, and
 |
(991) |
Finally, making use of (967), the Lagrangian of the Earth is written
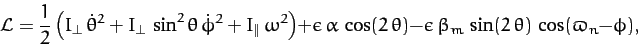 |
(992) |
where any constant terms have been neglected. Recall that 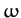 is given by (968), and is a constant of the motion.
is given by (968), and is a constant of the motion.
Two equations of motion that can immediately be derived from the above Lagrangian are
(The third equation, involving 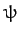 , merely confirms that
, merely confirms that 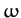 is a constant of the motion.)
The above two equations yield
is a constant of the motion.)
The above two equations yield
respectively.
Let
where
 is the mean inclination of the ecliptic to the Earth's equatorial plane. To first order in
is the mean inclination of the ecliptic to the Earth's equatorial plane. To first order in 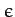 ,
Equations (995) and (996) reduce to
,
Equations (995) and (996) reduce to
respectively, where use has been made of Equation (983).
However, as can easily be verified after the fact,
 ,
so we obtain
,
so we obtain
The above equations can be integrated, and then combined with
Equations (997) and (998), to give
where
Incidentally, in the above, we have assumed that the lunar ascending node coincides with the vernal
equinox at time  (i.e.,
(i.e., 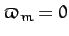 at
at  ), in accordance with our previous assumption that
), in accordance with our previous assumption that  at
at  .
.
According to Equation (1003), the combined gravitational interaction of the Sun and the Moon with the
quadrupole field generated by the Earth's slight oblateness causes the Earth's axis of rotation to
precess steadily about the normal to the ecliptic plane at the rate 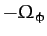 .
As before, the negative sign indicates that the precession is in the opposite direction to the (apparent) orbital
motion of the sun and moon. The period of the precession in years is given by
.
As before, the negative sign indicates that the precession is in the opposite direction to the (apparent) orbital
motion of the sun and moon. The period of the precession in years is given by
![\begin{displaymath}
T_\phi({\rm yr}) = \frac{n_s}{\Omega_\phi} = \frac{2\,T_s({\rm day})}{\epsilon\,(1+\mu_m/[T_m({\rm yr})]^2)\,\cos\theta_0},
\end{displaymath}](img2361.png) |
(1008) |
where
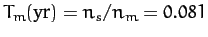 is the Moon's (synodic) orbital period in years. Given
that
is the Moon's (synodic) orbital period in years. Given
that
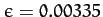 ,
,
 ,
,
 , and
, and 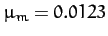 , we
obtain
, we
obtain
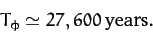 |
(1009) |
This prediction is fairly close to the observed precession period of
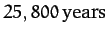 . The main reason that our estimate is slightly inaccurate is because we have neglected to take into
account the small eccentricities of the Earth's orbit around the Sun, and the Moon's orbit around
the Earth.
. The main reason that our estimate is slightly inaccurate is because we have neglected to take into
account the small eccentricities of the Earth's orbit around the Sun, and the Moon's orbit around
the Earth.
The point in the sky
toward which the Earth's axis of rotation points is known as the north celestial pole. Currently,
this point lies within about a degree of the fairly bright star Polaris, which is consequently sometimes known as the north star
or the pole star. It follows that Polaris appears to be almost stationary in the sky, always lying due north, and can thus
be used for navigational purposes. Indeed, mariners have relied on the north star for many hundreds
of years to determine direction at sea. Unfortunately, because of the precession of the
Earth's axis of rotation, the north celestial pole is not a fixed point in the sky, but instead traces out a circle,
of angular radius 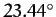 , about the north ecliptic pole, with a period of 25,800 years.
Hence, a few thousand years from now, the north celestial pole will no longer coincide with Polaris, and
there will be no convenient way of telling direction from the stars.
, about the north ecliptic pole, with a period of 25,800 years.
Hence, a few thousand years from now, the north celestial pole will no longer coincide with Polaris, and
there will be no convenient way of telling direction from the stars.
The projection of the ecliptic plane onto the sky is called the ecliptic, and coincides with the
apparent path of the Sun against the backdrop of the stars. Furthermore, the projection of the Earth's equator
onto the sky is known as the celestial equator. As has been previously mentioned, the ecliptic is inclined at 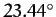 to the
celestial equator. The two points in the sky at which the ecliptic crosses the celestial equator are
called the equinoxes, since night and day are equally
long when the Sun lies at these points. Thus, the Sun reaches the vernal equinox on about
March 21st, and this traditionally marks the beginning of spring. Likewise, the Sun reaches the
autumn equinox on about September 22nd, and this traditionally marks the beginning of autumn.
However, the precession of the Earth's axis of rotation causes the
celestial equator (which is always normal to this axis) to precess in the sky, and thus also causes the equinoxes to precess along the ecliptic. This
effect is known as the precession of the equinoxes. The precession is in the opposite direction to the Sun's apparent motion around the ecliptic, and is of magnitude
to the
celestial equator. The two points in the sky at which the ecliptic crosses the celestial equator are
called the equinoxes, since night and day are equally
long when the Sun lies at these points. Thus, the Sun reaches the vernal equinox on about
March 21st, and this traditionally marks the beginning of spring. Likewise, the Sun reaches the
autumn equinox on about September 22nd, and this traditionally marks the beginning of autumn.
However, the precession of the Earth's axis of rotation causes the
celestial equator (which is always normal to this axis) to precess in the sky, and thus also causes the equinoxes to precess along the ecliptic. This
effect is known as the precession of the equinoxes. The precession is in the opposite direction to the Sun's apparent motion around the ecliptic, and is of magnitude 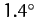 per century. Amazingly, this miniscule
effect was discovered by the Ancient Greeks (with the help of ancient Babylonian observations). In about 2000 BC, when the science of astronomy originated in ancient Egypt and Babylonia, the vernal equinox lay in the constellation Aries. Indeed, the
vernal equinox is still sometimes called the first point of Aries in astronomical texts. About 90 BC,
the vernal equinox moved into the constellation Pisces, where it still remains. The equinox will move
into the constellation Aquarius (marking the beginning of the much heralded ``Age of Aquarius'') in about 2600 AD. Incidentally, the position of the vernal equinox in the
sky is of great significance in astronomy, since it is used as the zero of celestial longitude (much as
Greenwich is used as the zero of terrestrial longitude).
per century. Amazingly, this miniscule
effect was discovered by the Ancient Greeks (with the help of ancient Babylonian observations). In about 2000 BC, when the science of astronomy originated in ancient Egypt and Babylonia, the vernal equinox lay in the constellation Aries. Indeed, the
vernal equinox is still sometimes called the first point of Aries in astronomical texts. About 90 BC,
the vernal equinox moved into the constellation Pisces, where it still remains. The equinox will move
into the constellation Aquarius (marking the beginning of the much heralded ``Age of Aquarius'') in about 2600 AD. Incidentally, the position of the vernal equinox in the
sky is of great significance in astronomy, since it is used as the zero of celestial longitude (much as
Greenwich is used as the zero of terrestrial longitude).
Equations (1003) and (1004) indicate that the small inclination of the lunar orbit to the ecliptic
plane, combined with the precession of the lunar ascending node, causes the Earth's axis of rotation to wobble
sightly. This wobble is known as nutation, and is superimposed on the aforementioned precession. In the absence of
precession, nutation would
cause the north celestial pole to periodically trace out a small ellipse on the sky, the sense of rotation being
counter-clockwise. The
nutation period is 18.6 years: i.e., the same as the precession period of the lunar ascending node.
The nutation amplitudes in the polar and azimuthal angles  and
and 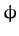 are
are
respectively, where
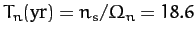 . Given
that
. Given
that
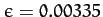 ,
,
 ,
,
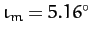 ,
,
 ,
,
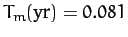 , and
, and 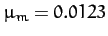 , we
obtain
, we
obtain
The observed nutation amplitudes are 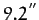 and
and 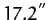 , respectively. Hence, our estimates are quite close to the
mark. Any inaccuracy is mainly due to the fact that we have neglected to take into
account the small eccentricities of the Earth's orbit around the Sun, and the Moon's orbit around
the Earth. The nutation of the Earth was discovered in 1728 by the English astronomer James Bradley, and
was explained theoretically about 20 years later by d'Alembert and L. Euler. Nutation is important because the corresponding gyration
of the Earth's rotation axis appears to be transferred to celestial objects when they are viewed using terrestrial
telescopes. This effect causes the celestial longitudes and latitudes of heavenly objects to oscillate sinusoidally by up to
, respectively. Hence, our estimates are quite close to the
mark. Any inaccuracy is mainly due to the fact that we have neglected to take into
account the small eccentricities of the Earth's orbit around the Sun, and the Moon's orbit around
the Earth. The nutation of the Earth was discovered in 1728 by the English astronomer James Bradley, and
was explained theoretically about 20 years later by d'Alembert and L. Euler. Nutation is important because the corresponding gyration
of the Earth's rotation axis appears to be transferred to celestial objects when they are viewed using terrestrial
telescopes. This effect causes the celestial longitudes and latitudes of heavenly objects to oscillate sinusoidally by up to 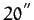 (i.e., about the maximum angular size of Saturn) with a period
of 18.6years. It is necessary to correct for this oscillation in order to accurately guide terrestrial telescopes
to particular objects.
(i.e., about the maximum angular size of Saturn) with a period
of 18.6years. It is necessary to correct for this oscillation in order to accurately guide terrestrial telescopes
to particular objects.
Note, finally, that the type of forced nutation discussed above, which is driven by an external torque, is
quite distinct from the free nutation described in Section 8.9.



Next: Potential Due to a
Up: Gravitational Potential Theory
Previous: Roche Radius
Richard Fitzpatrick
2011-03-31

![]() be the Earth's angular velocity vector due to its
daily rotation. This vector makes an angle
be the Earth's angular velocity vector due to its
daily rotation. This vector makes an angle ![]() with the
with the ![]() -axis,
where
-axis,
where
![]() is the mean inclination of the ecliptic to the
Earth's equatorial plane. Suppose that the projection of
is the mean inclination of the ecliptic to the
Earth's equatorial plane. Suppose that the projection of
![]() onto the ecliptic plane subtends an angle
onto the ecliptic plane subtends an angle ![]() with the
with the ![]() -axis,
where
-axis,
where ![]() is measured in a counter-clockwise (looking from the north) sense--see Figure 45.
The orientation of the Earth's axis of rotation (which is, of course, parallel
to
is measured in a counter-clockwise (looking from the north) sense--see Figure 45.
The orientation of the Earth's axis of rotation (which is, of course, parallel
to
![]() ) is thus determined by the two angles
) is thus determined by the two angles ![]() and
and ![]() .
Note, however, that these two angles are also Euler angles, in
the sense given in Chapter 8. Let us examine the Earth-Sun
system at an instant in time,
.
Note, however, that these two angles are also Euler angles, in
the sense given in Chapter 8. Let us examine the Earth-Sun
system at an instant in time, ![]() , when
, when ![]() : i.e., when
: i.e., when
![]() lies in the
lies in the ![]() -
-![]() plane. At this particular instant, the
plane. At this particular instant, the ![]() -axis points towards the so-called vernal equinox,
which is defined as the point in the sky where the ecliptic plane crosses the projection of the Earth's
equator (i.e., the plane normal to
-axis points towards the so-called vernal equinox,
which is defined as the point in the sky where the ecliptic plane crosses the projection of the Earth's
equator (i.e., the plane normal to
![]() ) from south to north. A counter-clockwise (looking from the north) angle in the
ecliptic plane that is zero at the vernal equinox is generally known as an ecliptic longitude. Thus,
) from south to north. A counter-clockwise (looking from the north) angle in the
ecliptic plane that is zero at the vernal equinox is generally known as an ecliptic longitude. Thus, ![]() is the
Sun's ecliptic longitude.
is the
Sun's ecliptic longitude.
![\begin{displaymath}
U = M_s\,\Phi = - \frac{G\,M_s\,M}{a_s} + \frac{G\,M_s\,(I_\parallel-I_\perp)}{a_s^{\,3}}\,P_2[\cos(\gamma_s)],
\end{displaymath}](img2271.png)
![]() )
)
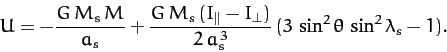
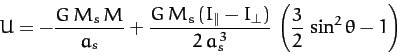
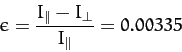
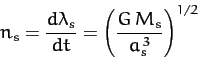
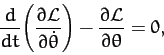
![]() , with both
, with both ![]() and
and ![]() constant. It follows, from the above equation, that
such motion must satisfy the constraint
constant. It follows, from the above equation, that
such motion must satisfy the constraint
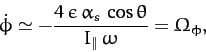
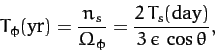
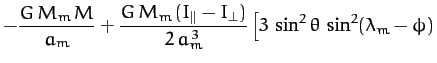

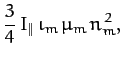
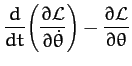
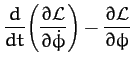
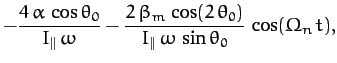
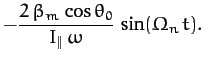
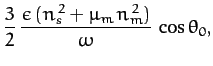
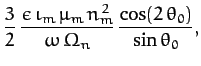
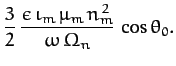
![]() .
As before, the negative sign indicates that the precession is in the opposite direction to the (apparent) orbital
motion of the sun and moon. The period of the precession in years is given by
.
As before, the negative sign indicates that the precession is in the opposite direction to the (apparent) orbital
motion of the sun and moon. The period of the precession in years is given by
![\begin{displaymath}
T_\phi({\rm yr}) = \frac{n_s}{\Omega_\phi} = \frac{2\,T_s({\rm day})}{\epsilon\,(1+\mu_m/[T_m({\rm yr})]^2)\,\cos\theta_0},
\end{displaymath}](img2361.png)
![]() , about the north ecliptic pole, with a period of 25,800 years.
Hence, a few thousand years from now, the north celestial pole will no longer coincide with Polaris, and
there will be no convenient way of telling direction from the stars.
, about the north ecliptic pole, with a period of 25,800 years.
Hence, a few thousand years from now, the north celestial pole will no longer coincide with Polaris, and
there will be no convenient way of telling direction from the stars.
![]() to the
celestial equator. The two points in the sky at which the ecliptic crosses the celestial equator are
called the equinoxes, since night and day are equally
long when the Sun lies at these points. Thus, the Sun reaches the vernal equinox on about
March 21st, and this traditionally marks the beginning of spring. Likewise, the Sun reaches the
autumn equinox on about September 22nd, and this traditionally marks the beginning of autumn.
However, the precession of the Earth's axis of rotation causes the
celestial equator (which is always normal to this axis) to precess in the sky, and thus also causes the equinoxes to precess along the ecliptic. This
effect is known as the precession of the equinoxes. The precession is in the opposite direction to the Sun's apparent motion around the ecliptic, and is of magnitude
to the
celestial equator. The two points in the sky at which the ecliptic crosses the celestial equator are
called the equinoxes, since night and day are equally
long when the Sun lies at these points. Thus, the Sun reaches the vernal equinox on about
March 21st, and this traditionally marks the beginning of spring. Likewise, the Sun reaches the
autumn equinox on about September 22nd, and this traditionally marks the beginning of autumn.
However, the precession of the Earth's axis of rotation causes the
celestial equator (which is always normal to this axis) to precess in the sky, and thus also causes the equinoxes to precess along the ecliptic. This
effect is known as the precession of the equinoxes. The precession is in the opposite direction to the Sun's apparent motion around the ecliptic, and is of magnitude ![]() per century. Amazingly, this miniscule
effect was discovered by the Ancient Greeks (with the help of ancient Babylonian observations). In about 2000 BC, when the science of astronomy originated in ancient Egypt and Babylonia, the vernal equinox lay in the constellation Aries. Indeed, the
vernal equinox is still sometimes called the first point of Aries in astronomical texts. About 90 BC,
the vernal equinox moved into the constellation Pisces, where it still remains. The equinox will move
into the constellation Aquarius (marking the beginning of the much heralded ``Age of Aquarius'') in about 2600 AD. Incidentally, the position of the vernal equinox in the
sky is of great significance in astronomy, since it is used as the zero of celestial longitude (much as
Greenwich is used as the zero of terrestrial longitude).
per century. Amazingly, this miniscule
effect was discovered by the Ancient Greeks (with the help of ancient Babylonian observations). In about 2000 BC, when the science of astronomy originated in ancient Egypt and Babylonia, the vernal equinox lay in the constellation Aries. Indeed, the
vernal equinox is still sometimes called the first point of Aries in astronomical texts. About 90 BC,
the vernal equinox moved into the constellation Pisces, where it still remains. The equinox will move
into the constellation Aquarius (marking the beginning of the much heralded ``Age of Aquarius'') in about 2600 AD. Incidentally, the position of the vernal equinox in the
sky is of great significance in astronomy, since it is used as the zero of celestial longitude (much as
Greenwich is used as the zero of terrestrial longitude).
![]() and
and ![]() are
are
![$\displaystyle \frac{3}{2}\,\frac{\epsilon\,\iota_m\,\mu_m\,T_n({\rm yr})}{T_s({\rm day})\,[T_m({\rm yr})]^2}\,\cos\theta_0,$](img2369.png)
![$\displaystyle \frac{3}{2}\,\frac{\epsilon\,\iota_m\,\mu_m\,T_n({\rm yr})}{T_s({\rm day})\,[T_m({\rm yr})]^2}\,\frac{\cos(2\,\theta_0)}{\sin\theta_0},$](img2370.png)