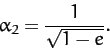Next: Kepler Problem
Up: Planetary Motion
Previous: Kepler's Third Law
According to Equations (215) and (223), the total energy per unit mass
of an object in orbit around the Sun is
given by
 |
(266) |
It follows from Equations (247), (251), and (256) that
![\begin{displaymath}
{\cal E} = \frac{h^2}{2}\left[\left(\frac{du}{d\theta}\right)^2
+ u^2 - 2\,u\,u_c\right],
\end{displaymath}](img771.png) |
(267) |
where 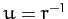 , and
, and
 . However, according to Equation (255),
. However, according to Equation (255),
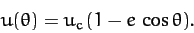 |
(268) |
The previous two equations can be combined with Equations (256)
and (259) to give
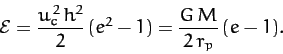 |
(269) |
We conclude that elliptical orbits (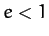 ) have negative total energies,
whereas parabolic orbits (
) have negative total energies,
whereas parabolic orbits (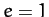 ) have zero total energies,
and hyperbolic orbits (
) have zero total energies,
and hyperbolic orbits (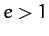 ) have positive total energies. This
makes sense, since in a conservative system in which the potential
energy at infinity is set to zero [see Equation (214)] we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies--see Section 3.2. Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun's gravitational field), and thus have zero total energy. For the special case of an elliptical orbit, whose major radius
) have positive total energies. This
makes sense, since in a conservative system in which the potential
energy at infinity is set to zero [see Equation (214)] we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies--see Section 3.2. Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun's gravitational field), and thus have zero total energy. For the special case of an elliptical orbit, whose major radius 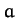 is finite, we can write
is finite, we can write
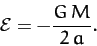 |
(270) |
It follows that the energy of such an orbit is completely determined by the orbital major radius.
Consider an artificial satellite in an elliptical orbit around the
Sun (the same considerations also apply to satellites in orbit around the Earth). At perihelion, 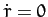 , and Equations (266) and (269)
can be combined to give
, and Equations (266) and (269)
can be combined to give
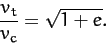 |
(271) |
Here,
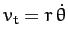 is the satellite's tangential velocity, and
is the satellite's tangential velocity, and
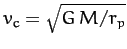 is the tangential velocity that it would need in order to
maintain a circular orbit at the perihelion distance.
Likewise, at aphelion,
is the tangential velocity that it would need in order to
maintain a circular orbit at the perihelion distance.
Likewise, at aphelion,
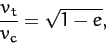 |
(272) |
where
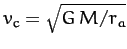 is now the tangential velocity that the
satellite would need in order to maintain a circular orbit at the aphelion distance.
is now the tangential velocity that the
satellite would need in order to maintain a circular orbit at the aphelion distance.
Suppose that our satellite is initially in a circular orbit of radius 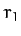 , and that we wish
to transfer it into a circular orbit of radius
, and that we wish
to transfer it into a circular orbit of radius 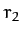 , where
, where 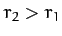 . We can
achieve this by temporarily placing the satellite in an elliptical orbit
whose perihelion distance is
. We can
achieve this by temporarily placing the satellite in an elliptical orbit
whose perihelion distance is 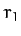 , and whose aphelion distance is
, and whose aphelion distance is 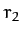 .
It follows, from Equation (262), that the required eccentricity of the elliptical
orbit is
.
It follows, from Equation (262), that the required eccentricity of the elliptical
orbit is
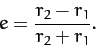 |
(273) |
According to Equation (271), we can transfer our satellite from its
initial circular orbit into the
temporary elliptical orbit by increasing its tangential velocity (by briefly
switching on the satellite's rocket motor) by a factor
 |
(274) |
We must next allow the satellite to execute half an orbit, so that it attains its aphelion
distance, and then boost the tangential velocity by a
factor [see Equation (272)]
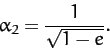 |
(275) |
The satellite will now be in a circular orbit at the aphelion distance, 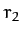 .
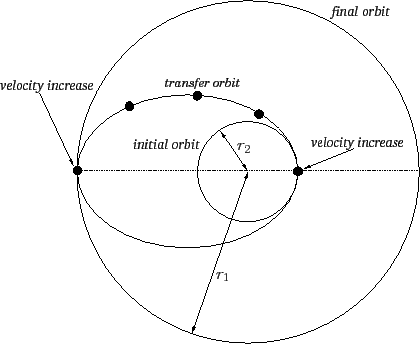
This process is illustrated in Figure 19. Obviously, we can transfer
our satellite from a larger to a smaller circular orbit by performing
the above process in reverse. Note, finally, from Equation (271), that if we
increase the tangential velocity of a satellite in a circular orbit about the Sun by a
factor greater than
.
This process is illustrated in Figure 19. Obviously, we can transfer
our satellite from a larger to a smaller circular orbit by performing
the above process in reverse. Note, finally, from Equation (271), that if we
increase the tangential velocity of a satellite in a circular orbit about the Sun by a
factor greater than 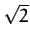 then we will transfer it into a
hyperbolic orbit (
then we will transfer it into a
hyperbolic orbit (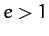 ), and it will eventually escape from the Sun's
gravitational field.
), and it will eventually escape from the Sun's
gravitational field.
Figure 19:
A transfer orbit between two circular orbits.
 |



Next: Kepler Problem
Up: Planetary Motion
Previous: Kepler's Third Law
Richard Fitzpatrick
2011-03-31

![]() , and Equations (266) and (269)
can be combined to give
, and Equations (266) and (269)
can be combined to give
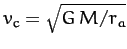 is now the tangential velocity that the
satellite would need in order to maintain a circular orbit at the aphelion distance.
is now the tangential velocity that the
satellite would need in order to maintain a circular orbit at the aphelion distance.
![]() , and that we wish
to transfer it into a circular orbit of radius
, and that we wish
to transfer it into a circular orbit of radius ![]() , where
, where ![]() . We can
achieve this by temporarily placing the satellite in an elliptical orbit
whose perihelion distance is
. We can
achieve this by temporarily placing the satellite in an elliptical orbit
whose perihelion distance is ![]() , and whose aphelion distance is
, and whose aphelion distance is ![]() .
It follows, from Equation (262), that the required eccentricity of the elliptical
orbit is
.
It follows, from Equation (262), that the required eccentricity of the elliptical
orbit is