


Next: Vector Algebra
Up: Vector Algebra and Vector
Previous: Introduction
Many physical quantities (e.g., mass, energy) are
entirely defined by a numerical magnitude (in appropriate units). Such quantities, which have no directional element, are
known as scalars. Moreover, since scalars can be represented by real numbers,
it follows that they obey the familiar laws of ordinary algebra. However, there exits a
second class of physical quantities (e.g., velocity, acceleration, force) which are
only completely defined when both a numerical magnitude and a direction in space is specified.
Such quantities are known as vectors. By definition, a vector obeys the same algebra as
a displacement in space, and may thus be represented geometrically by a
straight-line,
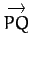 (say), where the arrow
indicates the direction of the displacement (i.e., from point
(say), where the arrow
indicates the direction of the displacement (i.e., from point 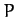 to point
to point 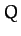 )--see Figure A.96.
The magnitude of the vector is represented by the length of the straight-line.
)--see Figure A.96.
The magnitude of the vector is represented by the length of the straight-line.
Figure A.96:
A vector.
 |
It is conventional to denote vectors by bold-faced symbols (e.g., 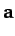 ,
, 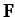 ) and
scalars by non-bold-faced symbols (e.g.,
) and
scalars by non-bold-faced symbols (e.g., 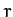 ,
, 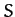 ). The magnitude of
a general vector,
). The magnitude of
a general vector, 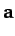 , is denoted
, is denoted 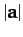 , or just
, or just 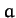 , and is, by definition, always
greater than or equal to zero. It is convenient to define a vector with zero magnitude--this is
denoted
, and is, by definition, always
greater than or equal to zero. It is convenient to define a vector with zero magnitude--this is
denoted 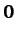 , and has no direction. Finally, two vectors,
, and has no direction. Finally, two vectors, 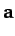 and
and 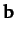 , are said
to be equal when their magnitudes and directions are identical.
, are said
to be equal when their magnitudes and directions are identical.
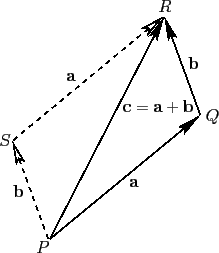
Figure A.97:
Vector addition.
 |



Next: Vector Algebra
Up: Vector Algebra and Vector
Previous: Introduction
Richard Fitzpatrick
2011-03-31

![]() ,
, ![]() ) and
scalars by non-bold-faced symbols (e.g.,
) and
scalars by non-bold-faced symbols (e.g., ![]() ,
, ![]() ). The magnitude of
a general vector,
). The magnitude of
a general vector, ![]() , is denoted
, is denoted ![]() , or just
, or just ![]() , and is, by definition, always
greater than or equal to zero. It is convenient to define a vector with zero magnitude--this is
denoted
, and is, by definition, always
greater than or equal to zero. It is convenient to define a vector with zero magnitude--this is
denoted ![]() , and has no direction. Finally, two vectors,
, and has no direction. Finally, two vectors, ![]() and
and ![]() , are said
to be equal when their magnitudes and directions are identical.
, are said
to be equal when their magnitudes and directions are identical.