

Next: Lagrange Points
Up: The Three-Body Problem
Previous: Tisserand Criterion
Let us transform to a non-inertial frame of reference rotating with angular
velocity 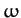 about an axis normal
to the orbital plane of masses
about an axis normal
to the orbital plane of masses 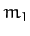 and
and 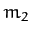 , and passing through their center of mass.
It
follows that masses
, and passing through their center of mass.
It
follows that masses 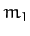 and
and 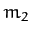 appear stationary in this new reference frame.
Let us define a Cartesian coordinate system
appear stationary in this new reference frame.
Let us define a Cartesian coordinate system 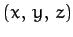 in the rotating frame of reference which is
such that masses
in the rotating frame of reference which is
such that masses 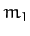 and
and 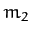 always lie on the
always lie on the 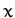 -axis, and the
-axis, and the 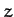 -axis
is parallel to the previously defined
-axis
is parallel to the previously defined 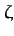 -axis. It follows that masses
-axis. It follows that masses
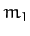 and
and 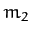 have the fixed position vectors
have the fixed position vectors
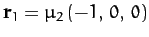 and
and
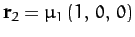 in our new coordinate system. Finally, let the position vector of
mass
in our new coordinate system. Finally, let the position vector of
mass 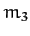 be
be
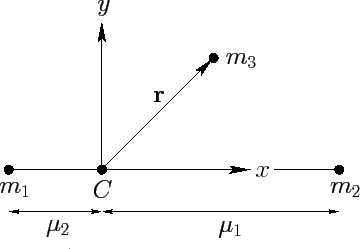
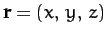 --see Figure 48.
--see Figure 48.
Figure 48:
The co-rotating frame.
 |
According to Chapter 7, the equation of motion of mass 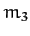 in the rotating
reference frame takes the form
in the rotating
reference frame takes the form
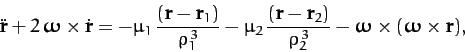 |
(1050) |
where
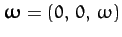 , and
, and
Here, the second term on the left-hand side of Equation (1050) is the Coriolis acceleration,
whereas the final term on the right-hand side is the centrifugal acceleration. The components of Equation (1050)
reduce to
which yield
where
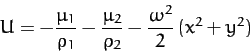 |
(1059) |
is the sum of the gravitational and centrifugal potentials.
Now, it follows from Equations (1056)-(1058) that
Summing the above three equations, we obtain
![\begin{displaymath}
\frac{d}{dt}\left[\frac{1}{2}\left(\dot{x}^2+\dot{y}^2+\dot{z}^2\right) + U\right] = 0.
\end{displaymath}](img2555.png) |
(1063) |
In other words,
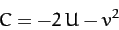 |
(1064) |
is a constant of the motion, where
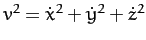 . In fact,
. In fact, 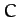 is the
Jacobi integral introduced in Section 13.3 [it is easily demonstrated that Equations (1039) and
(1064) are identical].
Note, finally, that
the mass
is the
Jacobi integral introduced in Section 13.3 [it is easily demonstrated that Equations (1039) and
(1064) are identical].
Note, finally, that
the mass 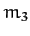 is restricted to regions in which
is restricted to regions in which
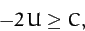 |
(1065) |
since 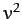 is a positive definite quantity.
is a positive definite quantity.


Next: Lagrange Points
Up: The Three-Body Problem
Previous: Tisserand Criterion
Richard Fitzpatrick
2011-03-31

![]() in the rotating
reference frame takes the form
in the rotating
reference frame takes the form
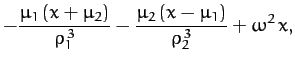
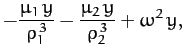
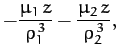
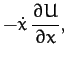
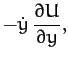
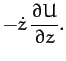
![\begin{displaymath}
\frac{d}{dt}\left[\frac{1}{2}\left(\dot{x}^2+\dot{y}^2+\dot{z}^2\right) + U\right] = 0.
\end{displaymath}](img2555.png)