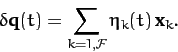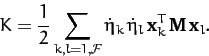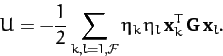Next: Spring-Coupled Masses
Up: Coupled Oscillations
Previous: Normal Modes
Since the eigenvectors 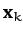 , for
, for 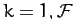 , span
, span 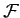 -dimensional
vector space, we can always write the displacement vector
-dimensional
vector space, we can always write the displacement vector 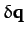 as some linear combination of the
as some linear combination of the 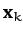 : i.e.,
: i.e.,
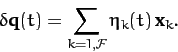 |
(808) |
We can regard the  as a new set of generalized coordinates,
since specifying the
as a new set of generalized coordinates,
since specifying the  is equivalent to specifying the
is equivalent to specifying the 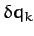 (and, hence, the
(and, hence, the  ). The
). The  are usually termed normal coordinates. According to Equations (799) and (808), the
normal coordinates can be written in terms of the
are usually termed normal coordinates. According to Equations (799) and (808), the
normal coordinates can be written in terms of the 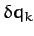 as
as
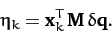 |
(809) |
Let us now try to express 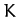 ,
,  , and the equations of motion
in terms of the
, and the equations of motion
in terms of the  .
.
The kinetic
energy can be written
 |
(810) |
where use has been made of Equation (775).
It follows from (808) that
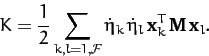 |
(811) |
Finally, making use of the orthonormality condition (799),
we obtain
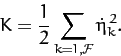 |
(812) |
Hence, the kinetic energy 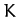 takes the form of a diagonal quadratic form when expressed in terms of the normal coordinates.
takes the form of a diagonal quadratic form when expressed in terms of the normal coordinates.
The potential energy can be written
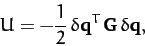 |
(813) |
where use has been made of Equations (780). It follows from (808) that
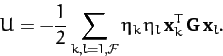 |
(814) |
Finally, making use of Equation (788) and the orthonormality condition (799),
we obtain
 |
(815) |
Hence, the potential energy  also takes the form of a diagonal quadratic form when expressed in terms of the normal coordinates.
also takes the form of a diagonal quadratic form when expressed in terms of the normal coordinates.
Writing Lagrange's equations of motion in terms of the normal
coordinates, we obtain [cf., Equation (772)]
 |
(816) |
for 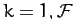 . Thus, it follows from Equations (812) and (815)
that
. Thus, it follows from Equations (812) and (815)
that
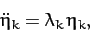 |
(817) |
for 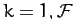 . In other words, Lagrange's equations reduce to a set of
. In other words, Lagrange's equations reduce to a set of
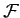 uncoupled simple harmonic equations when expressed in terms
of the normal coordinates. The solutions to the above equations are obvious:
i.e.,
uncoupled simple harmonic equations when expressed in terms
of the normal coordinates. The solutions to the above equations are obvious:
i.e.,
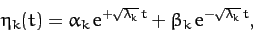 |
(818) |
where 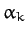 and
and 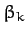 are arbitrary constants. Hence, it is clear from Equations (808) and (818) that the most general solution to
the perturbed equations of motion is indeed given by Equations (800)
and (801).
are arbitrary constants. Hence, it is clear from Equations (808) and (818) that the most general solution to
the perturbed equations of motion is indeed given by Equations (800)
and (801).
In conclusion, the equations of motion of a many degree of
freedom dynamical system which is slightly perturbed from an equilibrium state take a particularly simple form when expressed
in terms of the normal coordinates. Each normal
coordinate specifies the instantaneous displacement of an independent
mode of oscillation (or secular growth) of the system. Moreover, each
normal coordinate oscillates at a characteristic frequency (or grows at a characteristic rate), and is completely unaffected by the other coordinates.



Next: Spring-Coupled Masses
Up: Coupled Oscillations
Previous: Normal Modes
Richard Fitzpatrick
2011-03-31