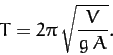Next: Multi-Dimensional Motion
Up: One-Dimensional Motion
Previous: Simple Pendulum
- If a train of mass
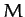 is subject to a retarding force
is subject to a retarding force 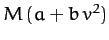 , show that if
the engines are shut off when the speed is
, show that if
the engines are shut off when the speed is 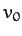 then the train will
come to rest in a time
then the train will
come to rest in a time
after traveling a distance
- A particle is projected vertically upward from the Earth's surface with a
velocity which would, if gravity were uniform, carry it to a height
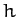 .
Show that if the variation of gravity with height is allowed for, but the
resistance of air is neglected, then the height reached will be greater by
.
Show that if the variation of gravity with height is allowed for, but the
resistance of air is neglected, then the height reached will be greater by 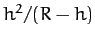 , where
, where
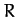 is the Earth's radius.
is the Earth's radius.
- A particle is projected vertically upward from the Earth's surface with a velocity
just sufficient for it to reach infinity (neglecting air resistance). Prove that the time needed to
reach a height
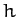 is
is
where 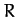 is the Earth's radius, and
is the Earth's radius, and 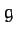 its surface gravitational acceleration.
its surface gravitational acceleration.
- A particle of mass
 is constrained to move in one dimension such that its instantaneous displacement is
is constrained to move in one dimension such that its instantaneous displacement is 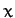 . The particle is
released at rest from
. The particle is
released at rest from  , and is
subject to a force of the form
, and is
subject to a force of the form
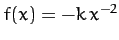 . Show that the time required
for the particle to reach the origin is
. Show that the time required
for the particle to reach the origin is
- A block of mass
 slides along a horizontal surface which is lubricated with
heavy oil such that the block suffers a viscous retarding force
of the form
slides along a horizontal surface which is lubricated with
heavy oil such that the block suffers a viscous retarding force
of the form
where 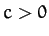 is a constant, and
is a constant, and 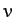 is the block's instantaneous velocity.
If the initial speed is
is the block's instantaneous velocity.
If the initial speed is 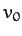 at time
at time  , find
, find 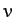 and the displacement
and the displacement
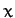 as functions of time
as functions of time 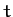 . Also find
. Also find 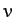 as a function of
as a function of 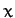 . Show
that for
. Show
that for 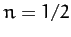 the block does not travel further than
the block does not travel further than
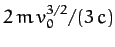 .
.
- A particle is projected vertically upward in a constant gravitational
field with an initial speed
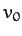 . Show that if there is a retarding force
proportional to the square of the speed then the speed of the
particle when it returns to the initial position is
. Show that if there is a retarding force
proportional to the square of the speed then the speed of the
particle when it returns to the initial position is
where 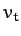 is the terminal speed.
is the terminal speed.
- A particle of mass
 moves (in one dimension) in a medium under the influence of a
retarding force of the form
moves (in one dimension) in a medium under the influence of a
retarding force of the form
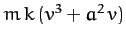 , where
, where 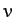 is the
particle speed, and
is the
particle speed, and  and
and  are positive constants. Show that
for any value of the initial speed the particle will
never move a distance greater than
are positive constants. Show that
for any value of the initial speed the particle will
never move a distance greater than 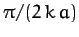 , and will only come to rest as
, and will only come to rest as
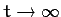 .
.
- Two light springs have spring constants
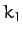 and
and 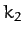 , respectively, and are used in a vertical
orientation to support an object of mass
, respectively, and are used in a vertical
orientation to support an object of mass  . Show that the angular frequency of oscillation
is
. Show that the angular frequency of oscillation
is
![$[(k_1+k_2)/m]^{1/2}$](img503.png) if the springs are in parallel, and
if the springs are in parallel, and
![$[k_1\,k_2/(k_1+k_2)\,m]^{1/2}$](img504.png) if the springs are in series.
if the springs are in series.
- A body of uniform cross-sectional area
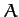 and mass density
and mass density  floats in a liquid
of density
floats in a liquid
of density 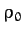 (where
(where 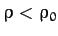 ), and at equilibrium displaces a volume
), and at equilibrium displaces a volume 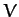 . Show
that the period of small oscillations about the equilibrium position is
. Show
that the period of small oscillations about the equilibrium position is
- Show that the ratio of two successive maxima in the displacement of a damped
harmonic oscillator is constant.
- If the amplitude of a damped harmonic oscillator decreases to
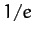 of its initial
value after
of its initial
value after  periods show that the ratio of the period of oscillation to the period
of the same oscillator with no damping is
periods show that the ratio of the period of oscillation to the period
of the same oscillator with no damping is
- Consider a damped driven oscillator whose equation of motion is
Let  and
and 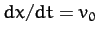 at
at  .
.
- Find the solution for
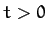 when
when
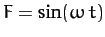 .
.
- Find the solution for
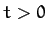 when
when
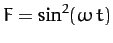 .
.
- Obtain the time asymptotic response of a damped linear oscillator of natural frequency
 and damping coefficient
and damping coefficient
 to a
square-wave periodic forcing function of amplitude
to a
square-wave periodic forcing function of amplitude
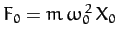 and frequency
and frequency  . Thus,
. Thus, 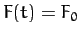 for
for
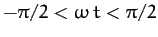 ,
,
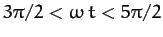 , etc., and
, etc., and
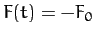 for
for
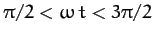 ,
,
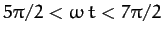 , etc.
, etc.



Next: Multi-Dimensional Motion
Up: One-Dimensional Motion
Previous: Simple Pendulum
Richard Fitzpatrick
2011-03-31
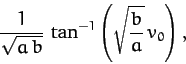

![\begin{displaymath}
\frac{1}{3}\left(\frac{2\,R}{g}\right)^{1/2}\,\left[\left(1+\frac{h}{R}\right)^{3/2}-1\right].
\end{displaymath}](img489.png)


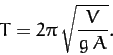

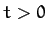 when
when
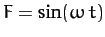 .
.
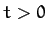 when
when
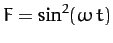 .
.
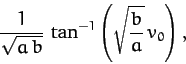

![\begin{displaymath}
\frac{1}{3}\left(\frac{2\,R}{g}\right)^{1/2}\,\left[\left(1+\frac{h}{R}\right)^{3/2}-1\right].
\end{displaymath}](img489.png)