


Next: Exercises
Up: One-Dimensional Motion
Previous: Transients
Simple Pendulum
Consider a compact mass 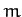 suspended from a light inextensible string of length
suspended from a light inextensible string of length 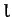 , such that the
mass is free to swing from side to side in a vertical plane, as shown in
Figure 9.
This setup is known as a simple pendulum.
Let
, such that the
mass is free to swing from side to side in a vertical plane, as shown in
Figure 9.
This setup is known as a simple pendulum.
Let 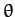 be the angle subtended between the string and
the downward vertical. Obviously, the stable equilibrium state of the simple pendulum corresponds to
the situation in which the mass is stationary, and hangs vertically down (i.e.,
be the angle subtended between the string and
the downward vertical. Obviously, the stable equilibrium state of the simple pendulum corresponds to
the situation in which the mass is stationary, and hangs vertically down (i.e., 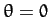 ).
From elementary mechanics, the angular equation of motion of the pendulum is
).
From elementary mechanics, the angular equation of motion of the pendulum is
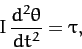 |
(138) |
where 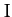 is the moment of inertia of the mass (see Section 8.3), and
is the moment of inertia of the mass (see Section 8.3), and 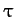 is the torque acting
about the pivot point (see Section A.7).
For the
case in hand, given that the mass is essentially a point particle, and is situated a distance
is the torque acting
about the pivot point (see Section A.7).
For the
case in hand, given that the mass is essentially a point particle, and is situated a distance 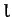 from
the axis of rotation (i.e., the pivot point), it is easily seen that
from
the axis of rotation (i.e., the pivot point), it is easily seen that
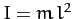 .
.
The two forces acting on the mass are the downward gravitational force, 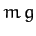 , where
, where 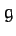 is the acceleration due to gravity,
and the tension,
is the acceleration due to gravity,
and the tension, 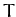 , in the string.
Note, however, that the tension makes no contribution to the torque,
since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance
, in the string.
Note, however, that the tension makes no contribution to the torque,
since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance 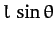 from the
pivot point. Hence, the magnitude of the gravitational torque is
from the
pivot point. Hence, the magnitude of the gravitational torque is
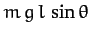 .
Moreover, the gravitational torque is a restoring torque: i.e., if
the mass is
displaced slightly from its equilibrium state (i.e.,
.
Moreover, the gravitational torque is a restoring torque: i.e., if
the mass is
displaced slightly from its equilibrium state (i.e., 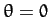 ) then the
gravitational torque clearly acts
to push the mass back toward that state. Thus, we can write
) then the
gravitational torque clearly acts
to push the mass back toward that state. Thus, we can write
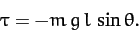 |
(139) |
Combining the previous two equations, we obtain the following angular equation
of motion of the pendulum:
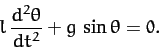 |
(140) |
Note that, unlike all of the other equations of motion which we have
examined in this chapter, the above equation is nonlinear [since
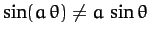 , except when
, except when 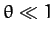 ].
].
Let us assume, as usual, that the system does not stray very far from
its equilibrium state (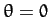 ). If this is the case then we
can make the small angle approximation
). If this is the case then we
can make the small angle approximation
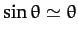 , and
the above equation of motion simplifies to
, and
the above equation of motion simplifies to
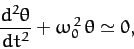 |
(141) |
where
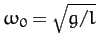 . Of course, this is just the
simple harmonic equation. Hence, we can immediately write the solution
as
. Of course, this is just the
simple harmonic equation. Hence, we can immediately write the solution
as
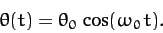 |
(142) |
We conclude that the pendulum swings back and forth at a fixed frequency, 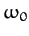 , which depends on
, which depends on 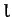 and
and 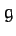 , but is independent of the amplitude,
, but is independent of the amplitude,
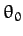 , of the motion.
, of the motion.
Suppose, now, that we desire a more accurate solution of Equation (140).
One way in which we could achieve this would be to include
more terms in the small angle expansion of 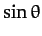 , which is
, which is
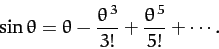 |
(143) |
For instance, keeping the first two terms in this expansion, Equation (140)
becomes
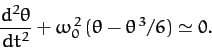 |
(144) |
By analogy with (142), let us try a trial solution of the
form
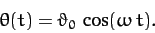 |
(145) |
Substituting this into Equation (144),
and making use of the trigonometric identity
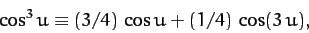 |
(146) |
we obtain
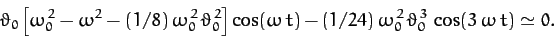 |
(147) |
It is evident that the above equation cannot be satisfied for all values of 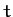 ,
except in the trivial case
,
except in the trivial case 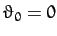 . However, the
form of this expression does suggest a better trial solution, namely
. However, the
form of this expression does suggest a better trial solution, namely
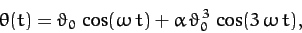 |
(148) |
where 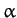 is
is 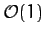 . Substitution of this expression into
Equation (144) yields
. Substitution of this expression into
Equation (144) yields
We can only satisfy the above equation at all values of 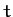 , and for non-zero
, and for non-zero 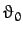 , by setting the two expressions in square brackets to zero.
This yields
, by setting the two expressions in square brackets to zero.
This yields
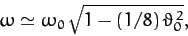 |
(150) |
and
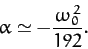 |
(151) |
Now, the amplitude of the motion is given by
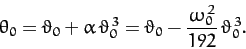 |
(152) |
Hence, Equation (150) simplifies to
![\begin{displaymath}
\omega = \omega_0\left[1-\frac{\theta_0^{\,2}}{16} + {\cal O}(\theta_0^{\,4})\right].
\end{displaymath}](img482.png) |
(153) |
The above expression is only approximate, but it illustrates an important
point: i.e., that the frequency of oscillation of a simple pendulum
is not, in fact, amplitude independent. Indeed, the frequency
goes down slightly as the amplitude increases.
The above example illustrates how we might go about solving a
nonlinear equation of motion by means of an expansion in a
small parameter (in this case, the amplitude of the motion).



Next: Exercises
Up: One-Dimensional Motion
Previous: Transients
Richard Fitzpatrick
2011-03-31
![]() , where
, where ![]() is the acceleration due to gravity,
and the tension,
is the acceleration due to gravity,
and the tension, ![]() , in the string.
Note, however, that the tension makes no contribution to the torque,
since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance
, in the string.
Note, however, that the tension makes no contribution to the torque,
since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance ![]() from the
pivot point. Hence, the magnitude of the gravitational torque is
from the
pivot point. Hence, the magnitude of the gravitational torque is
![]() .
Moreover, the gravitational torque is a restoring torque: i.e., if
the mass is
displaced slightly from its equilibrium state (i.e.,
.
Moreover, the gravitational torque is a restoring torque: i.e., if
the mass is
displaced slightly from its equilibrium state (i.e., ![]() ) then the
gravitational torque clearly acts
to push the mass back toward that state. Thus, we can write
) then the
gravitational torque clearly acts
to push the mass back toward that state. Thus, we can write
![]() ). If this is the case then we
can make the small angle approximation
). If this is the case then we
can make the small angle approximation
![]() , and
the above equation of motion simplifies to
, and
the above equation of motion simplifies to
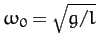 . Of course, this is just the
simple harmonic equation. Hence, we can immediately write the solution
as
. Of course, this is just the
simple harmonic equation. Hence, we can immediately write the solution
as
![]() , which is
, which is
![\begin{displaymath}
\omega = \omega_0\left[1-\frac{\theta_0^{\,2}}{16} + {\cal O}(\theta_0^{\,4})\right].
\end{displaymath}](img482.png)