


Next: Description of Lunar Motion
Up: Lunar Motion
Previous: Unperturbed Lunar Motion
The perturbed nonlinear lunar equations of motion, (1151)-(1153), take the general form
where
Let us search for solutions of the general form
Substituting expressions (1172)-(1177) into Equations (1169)-(1171), it is easily demonstrated that
 |
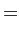 |
 |
(1178) |
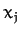 |
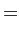 |
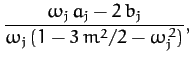 |
(1179) |
 |
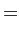 |
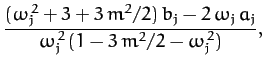 |
(1180) |
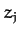 |
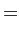 |
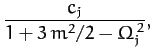 |
(1181) |
where 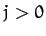 .
.
Table 3:
Angular frequencies and phase-shifts associated with the principal periodic driving terms appearing in
the perturbed nonlinear lunar equations of motion.
|
|
The angular frequencies, 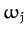 ,
, 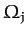 , and phase shifts,
, and phase shifts, 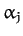 ,
, 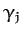 , of the principal periodic driving terms
that appear on the right-hand sides of the perturbed nonlinear lunar equations of motion, (1169)-(1171), are
specified in Table 3. Here,
, of the principal periodic driving terms
that appear on the right-hand sides of the perturbed nonlinear lunar equations of motion, (1169)-(1171), are
specified in Table 3. Here, 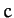 and
and 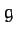 are, as yet, unspecified
are, as yet, unspecified 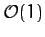 constants associated with
the precession of the lunar perigee, and the regression of the ascending node, respectively.
Note that
constants associated with
the precession of the lunar perigee, and the regression of the ascending node, respectively.
Note that 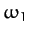 and
and 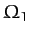 are the frequencies of the Moon's unforced motion in
ecliptic longitude and latitude, respectively. Moreover,
are the frequencies of the Moon's unforced motion in
ecliptic longitude and latitude, respectively. Moreover, 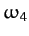 is the forcing frequency associated with the
perturbing influence of the Sun. All other frequencies appearing in Table 3 are combinations of these
three fundamental frequencies. In fact,
is the forcing frequency associated with the
perturbing influence of the Sun. All other frequencies appearing in Table 3 are combinations of these
three fundamental frequencies. In fact,
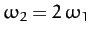 ,
,
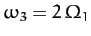 ,
,
 ,
,
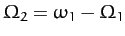 ,
,
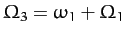 ,
and
,
and
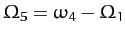 . Note that there is no
. Note that there is no 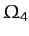 .
.
Now, a comparison of Equations (1151)-(1153), (1169)-(1171), and Table 1119 reveals that
Substitution of the solutions (1175)-(1177) into the above equations, followed by a comparison with expressions (1172)-(1174),
yields the amplitudes  ,
,  , and
, and 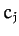 specified in Table 4. Note that, in calculating these amplitudes,
we have neglected all contributions to the periodic driving terms, appearing in Equations (1169)-(1171) which involve cubic, or higher order, combinations of
specified in Table 4. Note that, in calculating these amplitudes,
we have neglected all contributions to the periodic driving terms, appearing in Equations (1169)-(1171) which involve cubic, or higher order, combinations of 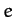 ,
, 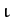 ,
, 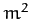 ,
, 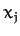 ,
, 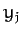 , and
, and  , since we only expanded Equations (1151)-(1153) to second-order in
, since we only expanded Equations (1151)-(1153) to second-order in 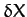 ,
, 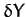 , and
, and 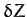 .
.
Table 4:
Amplitudes of the periodic driving terms appearing in the perturbed nonlinear lunar equations of motion.
| |
For 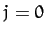 , it follows from Equation (1178) and Table 4 that
, it follows from Equation (1178) and Table 4 that
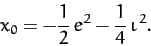 |
(1185) |
For 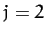 , making the approximation
, making the approximation
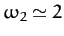 (see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
(see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
Likewise, making the approximation
 (see Table 3), it follows from Equation (1181)
and Table 4 that
(see Table 3), it follows from Equation (1181)
and Table 4 that
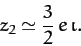 |
(1188) |
For 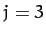 , making the approximation
, making the approximation
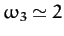 (see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
(see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
Likewise, making the approximation
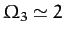 (see Table 3), it follows from Equation (1181)
and Table 4 that
(see Table 3), it follows from Equation (1181)
and Table 4 that
 |
(1191) |
For 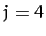 , making the approximation
, making the approximation
 (see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
(see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
Thus, according to Table 4,
For 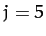 , making the approximation
, making the approximation
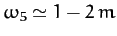 (see Table 3), it follows from Equations (1179), (1180), (1194), and (1195) that
(see Table 3), it follows from Equations (1179), (1180), (1194), and (1195) that
Likewise, making the approximation
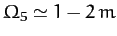 (see Table 3), it follows from Equations (1181)
and (1196) that
(see Table 3), it follows from Equations (1181)
and (1196) that
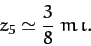 |
(1199) |
Thus, according to Table 4,
Finally, for 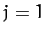 , by analogy with Equations (1160)-(1162), we expect
, by analogy with Equations (1160)-(1162), we expect
Thus, since
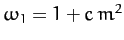 (see Table 3), it follows from Equations (1179), (1200), (1201),
and (1203)
that
(see Table 3), it follows from Equations (1179), (1200), (1201),
and (1203)
that
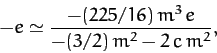 |
(1206) |
which yields
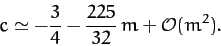 |
(1207) |
Likewise, since
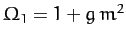 (see Table 3), it follows from Equations (1181), (1202), and (1205)
that
(see Table 3), it follows from Equations (1181), (1202), and (1205)
that
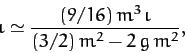 |
(1208) |
which yields
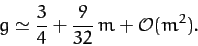 |
(1209) |
According to the above analysis, our final expressions for 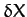 ,
, 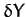 , and
, and 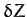 are
are
Thus, making use of Equations (1154)-(1156), we find that
The above expressions are accurate up to second-order in the small parameters 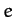 ,
, 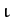 , and
, and  .
.



Next: Description of Lunar Motion
Up: Lunar Motion
Previous: Unperturbed Lunar Motion
Richard Fitzpatrick
2011-03-31
![]() ,
, ![]() , and phase shifts,
, and phase shifts, ![]() ,
, ![]() , of the principal periodic driving terms
that appear on the right-hand sides of the perturbed nonlinear lunar equations of motion, (1169)-(1171), are
specified in Table 3. Here,
, of the principal periodic driving terms
that appear on the right-hand sides of the perturbed nonlinear lunar equations of motion, (1169)-(1171), are
specified in Table 3. Here, ![]() and
and ![]() are, as yet, unspecified
are, as yet, unspecified ![]() constants associated with
the precession of the lunar perigee, and the regression of the ascending node, respectively.
Note that
constants associated with
the precession of the lunar perigee, and the regression of the ascending node, respectively.
Note that ![]() and
and ![]() are the frequencies of the Moon's unforced motion in
ecliptic longitude and latitude, respectively. Moreover,
are the frequencies of the Moon's unforced motion in
ecliptic longitude and latitude, respectively. Moreover, ![]() is the forcing frequency associated with the
perturbing influence of the Sun. All other frequencies appearing in Table 3 are combinations of these
three fundamental frequencies. In fact,
is the forcing frequency associated with the
perturbing influence of the Sun. All other frequencies appearing in Table 3 are combinations of these
three fundamental frequencies. In fact,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() . Note that there is no
. Note that there is no ![]() .
.
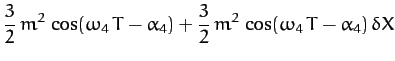
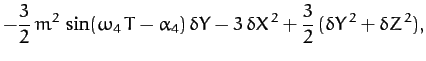

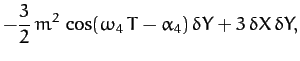
![]() , it follows from Equation (1178) and Table 4 that
, it follows from Equation (1178) and Table 4 that
![]() , making the approximation
, making the approximation
![]() (see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
(see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
![]() , making the approximation
, making the approximation
![]() (see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
(see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
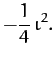
![]() , making the approximation
, making the approximation
![]() (see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
(see Table 3), it follows from Equations (1179), (1180)
and Table 4 that
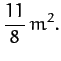
![]() , making the approximation
, making the approximation
![]() (see Table 3), it follows from Equations (1179), (1180), (1194), and (1195) that
(see Table 3), it follows from Equations (1179), (1180), (1194), and (1195) that
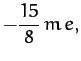
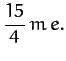
![]() , by analogy with Equations (1160)-(1162), we expect
, by analogy with Equations (1160)-(1162), we expect
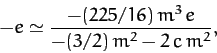
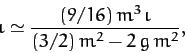
![]() ,
, ![]() , and
, and ![]() are
are
![$\displaystyle -\frac{1}{2}\,e^2-\frac{1}{4}\,\iota^2 - e\,\cos[(1+c\,m^2)\,T-\alpha_0] + \frac{1}{2}\,e^2\,\cos[2\,(1+c\,m^2)\,T-2\,\alpha_0]$](img2956.png)
![$\displaystyle + \frac{1}{4}\,\iota^2\,\cos[2\,(1+g\,m^2)\,T-2\,\gamma_0] - m^2\,\cos[2\,(1-m)\,T]$](img2957.png)
![$\displaystyle -\frac{15}{8}\,m\,e\,\cos[(1-2\,m-c\,m^2)\,T+\alpha_0],$](img2958.png)
![$\displaystyle 2\,e\,\sin[(1+c\,m^2)\,T-\alpha_0] + \frac{1}{4}\,e^2\,\sin[2\,(1+c\,m^2)\,T-2\,\alpha_0]$](img2959.png)
![$\displaystyle - \frac{1}{4}\,\iota^2\,\sin[2\,(1+g\,m^2)\,T-2\,\gamma_0] + \frac{11}{8}\,m^2\,\cos[2\,(1-m)\,T]$](img2960.png)
![$\displaystyle +\frac{15}{4}\,m\,e\,\sin[(1-2\,m-c\,m^2)\,T+\alpha_0],$](img2961.png)
![$\displaystyle \iota\,\sin[(1+g\,m^2)\,T-\gamma_0] + \frac{3}{2}\,e\,\iota\,\sin[(c-g)\,m^2\,T-\alpha_0+\gamma_0]$](img2962.png)
![$\displaystyle +\frac{1}{2}\,e\,\iota\,\sin [(2+c\,m^2+g\,m^2)\,T-\alpha_0-\gamma_0]$](img2963.png)
![$\displaystyle +\frac{3}{8}\,m\,\iota\,\sin[(1-2\,m-g\,m^2)\,T+\gamma_0].$](img2964.png)