


Next: Unperturbed Lunar Motion
Up: Lunar Motion
Previous: Preliminary Analysis
It is convenient to solve the lunar equation of motion, (1123), in a geocentric frame of reference, 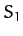 (say), which rotates with respect to
(say), which rotates with respect to
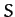 at the fixed angular velocity
at the fixed angular velocity
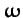 . Thus, if the lunar orbit were a circle, centered on the Earth, and lying in the ecliptic plane,
then the Moon would appear stationary in
. Thus, if the lunar orbit were a circle, centered on the Earth, and lying in the ecliptic plane,
then the Moon would appear stationary in 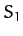 . In fact, the small eccentricity of the lunar orbit,
. In fact, the small eccentricity of the lunar orbit, 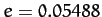 , combined
with its slight inclination to the ecliptic plane,
, combined
with its slight inclination to the ecliptic plane,
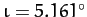 , causes the Moon to execute a small periodic orbit about the stationary point.
, causes the Moon to execute a small periodic orbit about the stationary point.
Let 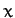 ,
, 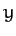 ,
, 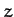 and
and 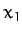 ,
, 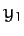 ,
, 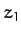 be the Cartesian coordinates
of the Moon in
be the Cartesian coordinates
of the Moon in 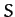 and
and 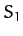 , respectively.
It is easily demonstrated that (see Section A.16)
, respectively.
It is easily demonstrated that (see Section A.16)
Moreover, if 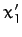 ,
, 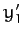 ,
, 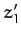 are the Cartesian components of the Sun in
are the Cartesian components of the Sun in 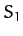 then (see Section A.5)
then (see Section A.5)
giving
where use has been made of Equations (1125)-(1127).
Now, in the rotating frame 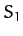 , the lunar equation of motion (1123) transforms to (see Chapter 7)
, the lunar equation of motion (1123) transforms to (see Chapter 7)
![\begin{displaymath}
\ddot{\bf r}+ 2\,\mbox{\boldmath$\omega$}\times\dot{\bf r} ...
...rt^{\,3}}
-\frac{{\bf r}'}{\vert{\bf r}'\vert^{\,3}}\right],
\end{displaymath}](img2740.png) |
(1137) |
where
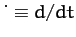 .
Furthermore, expanding the final term on the right-hand side of (1137) to lowest order in the small parameter
.
Furthermore, expanding the final term on the right-hand side of (1137) to lowest order in the small parameter 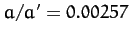 , we obtain
, we obtain
![\begin{displaymath}
\ddot{\bf r} +2\,\mbox{\boldmath$\omega$}\times\dot{\bf r}+...
...f r}')\,{\bf r}'}{\vert{\bf r}'\vert^{\,2}} - {\bf r}\right].
\end{displaymath}](img2742.png) |
(1138) |
When written in terms of Cartesian coordinates, the above equation yields
where
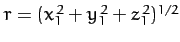 , and use has been made of Equations (1134)-(1136).
, and use has been made of Equations (1134)-(1136).
It is convenient, at this stage, to normalize all lengths to 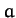 , and all times to
, and all times to 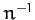 . Accordingly, let
. Accordingly, let
and
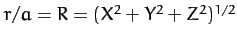 , and
, and 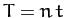 .
In normalized form, Equations (1139)-(1141) become
.
In normalized form, Equations (1139)-(1141) become
respectively,
where
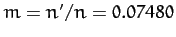 is a measure of the perturbing influence of the Sun on the lunar orbit. Here,
is a measure of the perturbing influence of the Sun on the lunar orbit. Here,
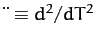 and
and
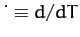 .
.
Finally, let us write
where
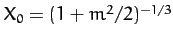 , and
, and 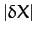 ,
, 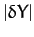 ,
,
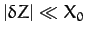 . Thus, if the lunar orbit were a circle,
centered on the Earth, and lying in the ecliptic plane,
then, in the rotating frame
. Thus, if the lunar orbit were a circle,
centered on the Earth, and lying in the ecliptic plane,
then, in the rotating frame 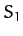 , the Moon would appear stationary at the point
, the Moon would appear stationary at the point 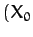 ,
, 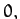
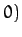 .
Expanding Equations (1145)-(1147) to second-order in
.
Expanding Equations (1145)-(1147) to second-order in 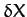 ,
, 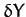 ,
,
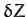 , and neglecting terms of order
, and neglecting terms of order 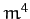 and
and
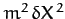 , etc., we obtain
, etc., we obtain
Now, once the above three equations have been solved for 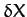 ,
, 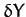 , and
, and 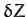 , the Cartesian coordinates,
, the Cartesian coordinates, 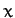 ,
, 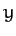 ,
, 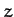 , of the Moon in the non-rotating geocentric
frame
, of the Moon in the non-rotating geocentric
frame 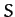 are obtained from Equations (1128)-(1130), (1142)-(1144), and (1148)-(1150). However, it is more convenient to write
are obtained from Equations (1128)-(1130), (1142)-(1144), and (1148)-(1150). However, it is more convenient to write
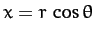 ,
,
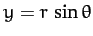 , and
, and
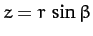 , where
, where 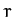 is the radial distance between the Earth and Moon, and
is the radial distance between the Earth and Moon, and 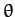 and
and 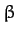 are termed the Moon's ecliptic
longitude and ecliptic latitude, respectively. Moreover, it is easily seen that, to second-order in
are termed the Moon's ecliptic
longitude and ecliptic latitude, respectively. Moreover, it is easily seen that, to second-order in 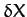 ,
, 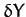 ,
,
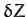 , and neglecting terms of order
, and neglecting terms of order 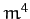 ,
,



Next: Unperturbed Lunar Motion
Up: Lunar Motion
Previous: Preliminary Analysis
Richard Fitzpatrick
2011-03-31
![]() ,
, ![]() ,
, ![]() and
and ![]() ,
, ![]() ,
, ![]() be the Cartesian coordinates
of the Moon in
be the Cartesian coordinates
of the Moon in ![]() and
and ![]() , respectively.
It is easily demonstrated that (see Section A.16)
, respectively.
It is easily demonstrated that (see Section A.16)
![]() , the lunar equation of motion (1123) transforms to (see Chapter 7)
, the lunar equation of motion (1123) transforms to (see Chapter 7)
![\begin{displaymath}
\ddot{\bf r} +2\,\mbox{\boldmath$\omega$}\times\dot{\bf r}+...
...f r}')\,{\bf r}'}{\vert{\bf r}'\vert^{\,2}} - {\bf r}\right].
\end{displaymath}](img2742.png)
![]() , and all times to
, and all times to ![]() . Accordingly, let
. Accordingly, let
![]() ,
, ![]() , and
, and ![]() , the Cartesian coordinates,
, the Cartesian coordinates, ![]() ,
, ![]() ,
, ![]() , of the Moon in the non-rotating geocentric
frame
, of the Moon in the non-rotating geocentric
frame ![]() are obtained from Equations (1128)-(1130), (1142)-(1144), and (1148)-(1150). However, it is more convenient to write
are obtained from Equations (1128)-(1130), (1142)-(1144), and (1148)-(1150). However, it is more convenient to write
![]() ,
,
![]() , and
, and
![]() , where
, where ![]() is the radial distance between the Earth and Moon, and
is the radial distance between the Earth and Moon, and ![]() and
and ![]() are termed the Moon's ecliptic
longitude and ecliptic latitude, respectively. Moreover, it is easily seen that, to second-order in
are termed the Moon's ecliptic
longitude and ecliptic latitude, respectively. Moreover, it is easily seen that, to second-order in ![]() ,
, ![]() ,
,
![]() , and neglecting terms of order
, and neglecting terms of order ![]() ,
,