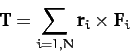Next: Exercises
Up: Newton's Laws of Motion
Previous: Newton's Third Law of
Non-Isolated Systems
Up to now, we have only considered isolated dynamical systems, in which all of the forces acting
on the system originate within the system itself. Let us now generalize our approach to
deal with non-isolated dynamical systems, in which some of the forces originate outside the system. Consider a system of 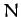 mutually interacting point objects. Let
mutually interacting point objects. Let
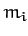 and
and 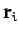 be the mass and position vector of the
be the mass and position vector of the  th object, respectively. Suppose
that the
th object, respectively. Suppose
that the  th object is subject to two forces. First, an internal force which originates
from the other objects in the system, and second an external force which originates
outside the system. In other words, let the force acting on the
th object is subject to two forces. First, an internal force which originates
from the other objects in the system, and second an external force which originates
outside the system. In other words, let the force acting on the  th object take the form
th object take the form
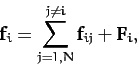 |
(38) |
where 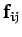 is the internal force exerted by object
is the internal force exerted by object 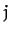 on object
on object  , and
, and 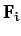 the
net external force acting on object
the
net external force acting on object  .
.
The equation of motion of the  th object is
th object is
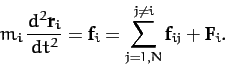 |
(39) |
Summing over all objects, we obtain
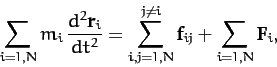 |
(40) |
which reduces to
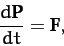 |
(41) |
where
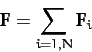 |
(42) |
is the net external force acting on the system. Here, the sum over the internal forces has cancelled out in pairs
due to Newton's third law of motion. We conclude that the total system momentum evolves in time according to the
simple equation (41)
when there is a net external force acting on the system, but is completely unaffected by the internal forces.
The fact that Equation (41) is similar in form to Equation (13) suggests that the center of
mass of a system of many point objects has analogous dynamics to a point object.
Taking
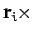 Equation (39), and summing over all objects, we obtain
Equation (39), and summing over all objects, we obtain
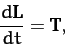 |
(43) |
where
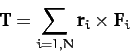 |
(44) |
is the net external torque acting on the system. Here, the sum over the internal
torques has cancelled out in pairs, assuming that the internal forces are central in nature.
We conclude that the total system angular momentum evolves in time according to the simple equation (43)
when there is a net external torque acting on the system, but is completely unaffected by the internal torques.



Next: Exercises
Up: Newton's Laws of Motion
Previous: Newton's Third Law of
Richard Fitzpatrick
2011-03-31
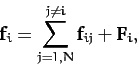
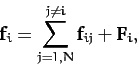
![]() th object is
th object is
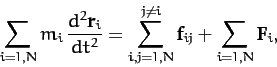
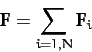
![]() Equation (39), and summing over all objects, we obtain
Equation (39), and summing over all objects, we obtain