

Next: Perihelion Precession of the
Up: Gravitational Potential Theory
Previous: Precession and Forced Nutation
Consider a uniform ring of mass 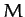 and radius
and radius 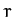 , centered on the origin, and lying in the
, centered on the origin, and lying in the 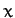 -
-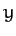 plane.
Let us consider the gravitational potential
plane.
Let us consider the gravitational potential 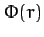 generated by such a ring in the
generated by such a ring in the 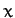 -
-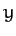 plane
(which corresponds to
plane
(which corresponds to
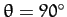 ). It follows, from Section 12.3, that for
). It follows, from Section 12.3, that for 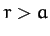 ,
,
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{a}{r}\right)^{n+1}.
\end{displaymath}](img2380.png) |
(1014) |
However, 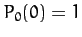 ,
, 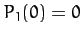 ,
, 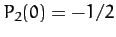 ,
, 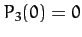 , and
, and 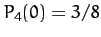 . Hence,
. Hence,
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{r}\left[1 + \frac{1}{4}\left(\frac{a...
...ght)^2 + \frac{9}{64}\left(\frac{a}{r}\right)^4+\cdots\right].
\end{displaymath}](img2386.png) |
(1015) |
Likewise, for 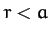 ,
,
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{r}{a}\right)^{n},
\end{displaymath}](img2388.png) |
(1016) |
giving
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{a}\left[1 + \frac{1}{4}\left(\frac{r...
...ght)^2 + \frac{9}{64}\left(\frac{r}{a}\right)^4+\cdots\right].
\end{displaymath}](img2389.png) |
(1017) |
Richard Fitzpatrick
2011-03-31
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{a}{r}\right)^{n+1}.
\end{displaymath}](img2380.png)
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{a}{r}\right)^{n+1}.
\end{displaymath}](img2380.png)
![\begin{displaymath}
\Phi(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{r}{a}\right)^{n},
\end{displaymath}](img2388.png)