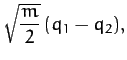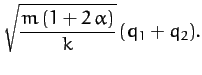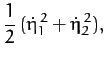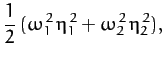Next: Exercises
Up: Coupled Oscillations
Previous: Spring-Coupled Masses
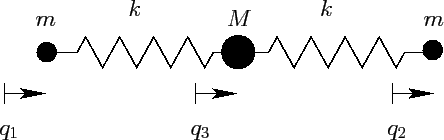
Consider the simple model of a linear triatomic molecule (e.g., carbon
dioxide) illustrated in Figure 38. The molecule consists
of a central atom of mass 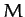 flanked by two identical atoms of
mass
flanked by two identical atoms of
mass  . The atomic bonds are represented as springs of spring constant
. The atomic bonds are represented as springs of spring constant  .
The linear displacements of the flanking atoms are
.
The linear displacements of the flanking atoms are  and
and 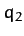 ,
whilst that of the central atom is
,
whilst that of the central atom is 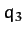 . Let us investigate the linear modes of oscillation our model molecule.
. Let us investigate the linear modes of oscillation our model molecule.
Figure 38:
A model triatomic molecule.
 |
The kinetic energy of the molecule is written
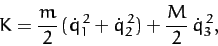 |
(840) |
whereas the potential energy takes the form
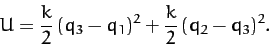 |
(841) |
Clearly, we have a three degree of freedom dynamical system. However, we
can reduce this to a two degree of freedom system by only considering
oscillatory modes of motion, and, hence, neglecting translational modes. We can achieve this by demanding that the center
of mass of the system remains stationary. In other words, we require that
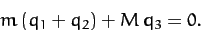 |
(842) |
This constraint can be rearranged to give
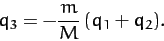 |
(843) |
Eliminating 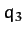 from Equations (840) and (841), we obtain
from Equations (840) and (841), we obtain
![\begin{displaymath}
K = \frac{m}{2}\left[(1+\alpha)\,\dot{q}_1^{\,2} + 2\,\alpha\,\dot{q}_1\,\dot{q}_2 + (1+\alpha)\,\dot{q}_2^{\,2}\right],
\end{displaymath}](img2033.png) |
(844) |
and
![\begin{displaymath}
U = \frac{k}{2}\left[(1+2\,\alpha+2\,\alpha^2)\,q_1^{\,2} + ...
...alpha)\,q_1\,q_2 +(1+2\,\alpha+2\,\alpha^2)\,q_2^{\,2}\right],
\end{displaymath}](img2034.png) |
(845) |
respectively, where 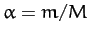 .
.
A comparison of the above expressions with the standard
forms (775) and (780) yields the following
expressions for the mass matrix, 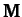 , and the force matrix,
, and the force matrix, 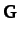 :
:
Now, the equation of motion of the system takes the form [see Equation (786)]
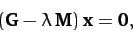 |
(848) |
where 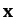 is the column vector of the
is the column vector of the  and
and 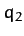 values.
The solubility condition for the above equation is
values.
The solubility condition for the above equation is
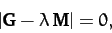 |
(849) |
which yields the following quadratic equation for the eigenvalue 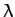 :
:
![\begin{displaymath}
(1+2\,\alpha)\,\left[m^2\,\lambda^2 + 2\,m\,k\,(1+\alpha)\,\lambda + k^2\,(1+2\alpha)\right] = 0.
\end{displaymath}](img2038.png) |
(850) |
The two roots of the above equation are
The fact that the roots are negative implies that both normal modes are indeed
oscillatory in nature. The characteristic oscillation frequencies are
Equation (848) can now be solved, subject to the normalization
condition (799), to give the two eigenvectors:
Thus, we conclude from Equations (843) and (853)-(856) that our model molecule possesses two normal modes of oscillation. The first mode oscillates at the frequency 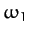 , and
is an anti-symmetric mode in which
, and
is an anti-symmetric mode in which 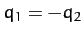 and
and 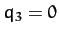 .
In other words, in this mode of oscillation, the two end atoms move in opposite
directions whilst the central atom remains stationary. The second mode oscillates at the frequency
.
In other words, in this mode of oscillation, the two end atoms move in opposite
directions whilst the central atom remains stationary. The second mode oscillates at the frequency 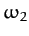 , and is a mixed symmetry mode in which
, and is a mixed symmetry mode in which
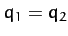 but
but
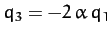 . In other words, in this mode of oscillation, the
two end atoms move in the same direction whilst the central atom moves
in the opposite direction.
. In other words, in this mode of oscillation, the
two end atoms move in the same direction whilst the central atom moves
in the opposite direction.
Finally, it is easily demonstrated that the normal coordinates of the system
are
When expressed in terms of these coordinates, 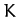 and
and  reduce to
reduce to
respectively.



Next: Exercises
Up: Coupled Oscillations
Previous: Spring-Coupled Masses
Richard Fitzpatrick
2011-03-31

![]() , and the force matrix,
, and the force matrix, ![]() :
:
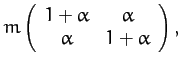
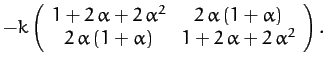
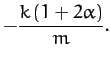
![]() , and
is an anti-symmetric mode in which
, and
is an anti-symmetric mode in which ![]() and
and ![]() .
In other words, in this mode of oscillation, the two end atoms move in opposite
directions whilst the central atom remains stationary. The second mode oscillates at the frequency
.
In other words, in this mode of oscillation, the two end atoms move in opposite
directions whilst the central atom remains stationary. The second mode oscillates at the frequency ![]() , and is a mixed symmetry mode in which
, and is a mixed symmetry mode in which
![]() but
but
![]() . In other words, in this mode of oscillation, the
two end atoms move in the same direction whilst the central atom moves
in the opposite direction.
. In other words, in this mode of oscillation, the
two end atoms move in the same direction whilst the central atom moves
in the opposite direction.