


Next: Axisymmetric Irrotational Flow in
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Stokes Stream Function
Axisymmetric Velocity Fields
According to the analysis of Appendix C, Equations (7.3) and (7.4) imply that
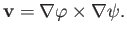 |
(7.5) |
When the fluid velocity is written in this form it becomes obvious
that the incompressibility constraint
 is
satisfied [because
is
satisfied [because
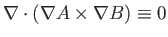 --see Equations (A.175) and (A.176)].
It is also clear that the Stokes stream function,
--see Equations (A.175) and (A.176)].
It is also clear that the Stokes stream function,  , is undefined to an arbitrary additive constant.
, is undefined to an arbitrary additive constant.
In fact, the most general expression for an axisymmetric incompressible flow pattern
is
 |
(7.6) |
where
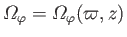 is the angular velocity of flow circulating about the
is the angular velocity of flow circulating about the  -axis.
(This follows because
-axis.
(This follows because
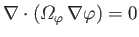 when
when
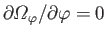 . See Appendix C.)
The previous expression implies that
. See Appendix C.)
The previous expression implies that
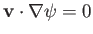 (because
(because
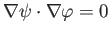 when
when
 ). In other words,
when plotted in the meridian plane, streamlines in a general axisymmetric flow pattern correspond to contours of
). In other words,
when plotted in the meridian plane, streamlines in a general axisymmetric flow pattern correspond to contours of  .
.
Making use of the vector identities (A.176) and (A.178), we can also write Equation (7.6) in the form
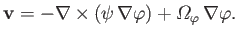 |
(7.7) |
It follows from the identity (A.177) that
because
 , by symmetry.
Hence, the vorticity of a general axisymmetric flow pattern is written
, by symmetry.
Hence, the vorticity of a general axisymmetric flow pattern is written
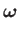 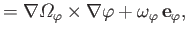 |
(7.9) |
where
 , and [see Equations (C.52)-(C.54)]
, and [see Equations (C.52)-(C.54)]
In the following, we shall concentrate on axisymmetric flow patterns in which there is no circulation about the  -axis
(i.e.,
-axis
(i.e.,
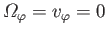 ).
).



Next: Axisymmetric Irrotational Flow in
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Stokes Stream Function
Richard Fitzpatrick
2016-03-31