


Next: Schwarz-Christoffel Theorem
Up: Two-Dimensional Potential Flow
Previous: Method of Images
Conformal Maps
Let
 and
and
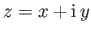 , where
, where 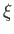 ,
,  ,
,  , and
, and  are real. Suppose that
are real. Suppose that
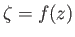 , where
, where 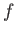 is a well-behaved (i.e., single-valued, non-singular, and differentiable) function. We can think
of
is a well-behaved (i.e., single-valued, non-singular, and differentiable) function. We can think
of
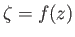 as a map from the complex
as a map from the complex  -plane to the complex
-plane to the complex 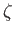 -plane. In other words, every point
-plane. In other words, every point
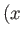 ,
,  in the complex
in the complex  -plane maps to a corresponding point
-plane maps to a corresponding point 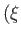 ,
,  in the complex
in the complex 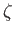 -plane. Moreover,
if
-plane. Moreover,
if  is indeed a well-behaved function then this mapping is unique, and also has a unique inverse. Suppose that the point
is indeed a well-behaved function then this mapping is unique, and also has a unique inverse. Suppose that the point 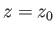 in the
in the  -plane maps to the point
-plane maps to the point
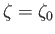 in the
in the 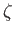 -plane. Let us investigate how neighboring points map.
We have
-plane. Let us investigate how neighboring points map.
We have
In other words, the points 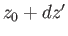 and
and 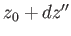 in the complex
in the complex  -plane map to the
points
-plane map to the
points
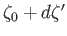 and
and
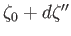 in the complex
in the complex 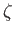 -plane, respectively. If
-plane, respectively. If 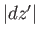 ,
,
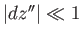 then
then
where
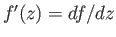 . Hence,
. Hence,
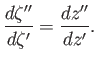 |
(6.57) |
Thus, it follows that
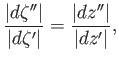 |
(6.58) |
and
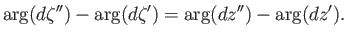 |
(6.59) |
We can think of 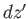 and
and 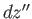 as infinitesimal vectors connecting neighboring points in the complex
as infinitesimal vectors connecting neighboring points in the complex  -plane
to the point
-plane
to the point 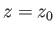 . Likewise,
. Likewise, 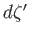 and
and 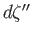 are infinitesimal vectors connecting the corresponding points in the complex
are infinitesimal vectors connecting the corresponding points in the complex 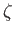 -plane. It is clear, from the previous two equations, that, in the vicinity of
-plane. It is clear, from the previous two equations, that, in the vicinity of 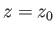 , the mapping from the complex
, the mapping from the complex  -plane to
the complex
-plane to
the complex 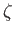 -plane is such that the lengths of
-plane is such that the lengths of 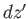 and
and 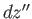 expand or contract by the same factor, and
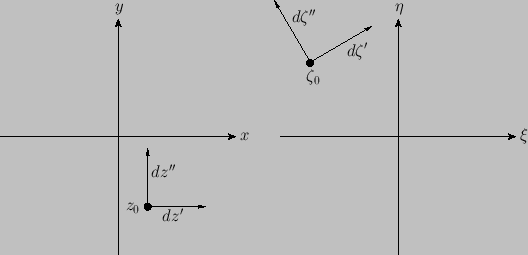
the angle subtended between these two vectors remains the same. (See Figure 6.7.) This type of mapping is termed conformal.
expand or contract by the same factor, and
the angle subtended between these two vectors remains the same. (See Figure 6.7.) This type of mapping is termed conformal.
Figure 6.7:
A conformal map.
 |
Suppose that
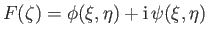 is a well-behaved function of the complex variable
is a well-behaved function of the complex variable 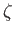 . It follows
that
. It follows
that
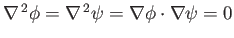 . Hence, the functions
. Hence, the functions
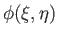 and
and
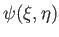 can be interpreted
as the velocity potential and stream function, respectively, of some two-dimensional, incompressible, irrotational flow pattern, where
can be interpreted
as the velocity potential and stream function, respectively, of some two-dimensional, incompressible, irrotational flow pattern, where 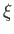 and
and
 are Cartesian coordinates.
However, if
are Cartesian coordinates.
However, if
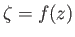 , where
, where  is well-behaved, then
is well-behaved, then
![$ F(\zeta)=F[f(z)] = G(z) = \widetilde{\phi}(x,y) + {\rm i}\,\widetilde{\psi}(x,y)$](img2086.png) , where
, where 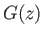 is also well-behaved. It follows that
is also well-behaved. It follows that
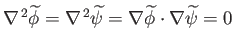 . In other words, the functions
. In other words, the functions
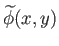 and
and
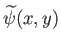 can be interpreted
as the velocity potential and stream function, respectively, of some new, two-dimensional, incompressible, irrotational flow pattern, where
can be interpreted
as the velocity potential and stream function, respectively, of some new, two-dimensional, incompressible, irrotational flow pattern, where  and
and
 are Cartesian coordinates. In other words, we can use a conformal map to convert a given two-dimensional, incompressible, irrotational flow pattern into another, quite different, pattern.
Incidentally, a conformal map converts a line source into a line source of the same strength, and a vortex filament into a vortex filament of the same intensity. (See Exercise 12.)
are Cartesian coordinates. In other words, we can use a conformal map to convert a given two-dimensional, incompressible, irrotational flow pattern into another, quite different, pattern.
Incidentally, a conformal map converts a line source into a line source of the same strength, and a vortex filament into a vortex filament of the same intensity. (See Exercise 12.)
As an example, consider the conformal map
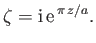 |
(6.60) |
Writing
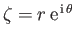 , it is easily demonstrated that
, it is easily demonstrated that
 and
and
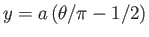 .
Hence, the positive
.
Hence, the positive 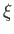 -axis (
-axis (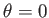 ) maps to the line
) maps to the line  , the negative
, the negative 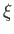 -axis (
-axis (
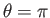 ) maps to the line
) maps to the line
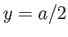 , and the region
, and the region  (
(
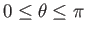 ) maps to the region
) maps to the region
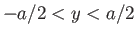 . Moreover, the points
. Moreover, the points
 ,
, 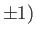 map to the points
map to the points 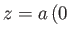 ,
,
 . (See Figure 6.8.) As we saw in Section 6.6,
in the region
. (See Figure 6.8.) As we saw in Section 6.6,
in the region  ,
the velocity potential
,
the velocity potential
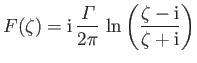 |
(6.61) |
corresponds to the flow pattern generated by a vortex filament of intensity
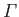 , located at the
point
, located at the
point  ,
, 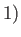 , in the presence of a rigid plane at
, in the presence of a rigid plane at 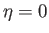 . Hence,
. Hence,
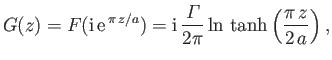 |
(6.62) |
corresponds to the flow pattern generated by a vortex filament of intensity
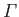 , located at the origin,
in the presence of two rigid planes at
, located at the origin,
in the presence of two rigid planes at 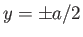 . This follows because the line
. This follows because the line 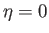 is mapped to
the lines
is mapped to
the lines 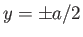 , and the point
, and the point  ,
, 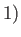 is mapped to the origin. Moreover, if the line
is mapped to the origin. Moreover, if the line 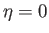 is a streamline in the
is a streamline in the  -plane then
the lines
-plane then
the lines 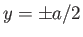 are also streamlines in the
are also streamlines in the  -plane. Thus, these lines could all correspond to rigid boundaries.
The stream function associated with the previous
complex velocity potential,
-plane. Thus, these lines could all correspond to rigid boundaries.
The stream function associated with the previous
complex velocity potential,
![$\displaystyle \psi(x,y)= \frac{{\mit\Gamma}}{\pi}\,\ln\left[\frac{\cosh(\pi\,x\,a)-\cos(\pi\,y/a) }{\cosh(\pi\,x/a)+\cos(\pi\,y/a)}\right],$](img2109.png) |
(6.63) |
is shown in Figure 6.9.
Figure:
The conformal map
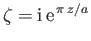 .
.
 |
Figure:
Stream lines of the two-dimensional flow pattern due to a vortex filament at the origin in the presence
of two rigid planes at 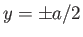 .
.
 |
As a second example, consider the map
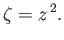 |
(6.64) |
This maps the positive 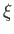 -axis to the positive
-axis to the positive  -axis, the negative
-axis, the negative 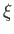 -axis to the positive
-axis to the positive  -axis, the
region
-axis, the
region  to the region
to the region  ,
, 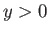 , and the point
, and the point  ,
,
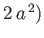 to the point
to the point 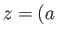 ,
, 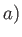 .
As we saw in Section 6.6,
in the region
.
As we saw in Section 6.6,
in the region  ,
the velocity potential
,
the velocity potential
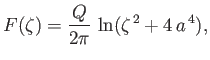 |
(6.65) |
corresponds to the flow pattern generated by a line source of strength  , located at the
point
, located at the
point
 ,
,
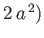 , in the presence of a rigid plane at
, in the presence of a rigid plane at 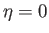 . Thus, the complex
velocity potential
. Thus, the complex
velocity potential
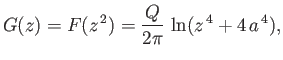 |
(6.66) |
corresponds to the flow pattern generated by a line source of strength  , located
at the point
, located
at the point 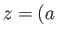 ,
, 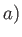 , in the presence of two orthogonal rigid planes at
, in the presence of two orthogonal rigid planes at  and
and  .
The stream function associated with the previous complex potential,
.
The stream function associated with the previous complex potential,
![$\displaystyle \psi(x,y) = -\frac{Q}{2\pi}\,\tan^{-1}\left[\frac{4\,x\,y\,(x^{\,2}-y^{\,2})}{x^{\,4}-6\,x^{\,2}\,y^{\,2}+y^{\,4}+4\,a^{\,4}}\right],$](img2119.png) |
(6.67) |
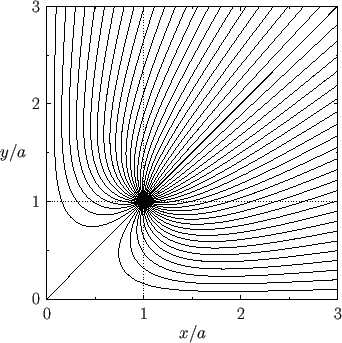
is shown in Figure 6.10.
Figure:
Stream lines of the two-dimensional flow pattern due to a line source at 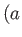 ,
, 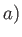 in the presence
of two rigid planes at
in the presence
of two rigid planes at  and
and  .
.
 |
As a final example, consider the map
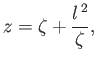 |
(6.68) |
where 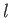 is real and positive. Writing
is real and positive. Writing
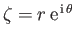 , we find that
, we find that
Thus, the map converts the circle
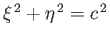 in the
in the 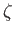 -plane, where
-plane, where 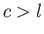 , into the ellipse
, into the ellipse
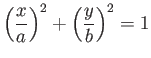 |
(6.71) |
in the  -plane,
where
-plane,
where
Note that the center of the ellipse lies at the origin, and its major and minor axes run parallel to the  - and the
- and the  -axes,
respectively. As we saw in Section 6.4, in the
-axes,
respectively. As we saw in Section 6.4, in the 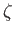 -plane, the complex velocity potential
-plane, the complex velocity potential
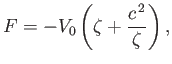 |
(6.74) |
represents uniform flow of unperturbed speed 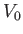 , running parallel to the
, running parallel to the 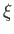 -axis, around a circular cylinder
of radius
-axis, around a circular cylinder
of radius 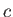 , centered on the origin. Thus, assuming that
, centered on the origin. Thus, assuming that 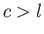 , in the
, in the  -plane, the potential represents uniform flow of unperturbed speed
-plane, the potential represents uniform flow of unperturbed speed 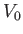 , running parallel to the
, running parallel to the  -axis [which follows because at large
-axis [which follows because at large 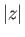 the map (6.68) reduces to
the map (6.68) reduces to 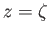 , and so the flow at large distances from the origin is the same in the complex
, and so the flow at large distances from the origin is the same in the complex  - and
- and 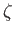 -planes], around
an elliptical cylinder of major radius
-planes], around
an elliptical cylinder of major radius  , aligned along the
, aligned along the  -axis, and minor
radius
-axis, and minor
radius 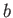 , aligned along the
, aligned along the  -axis. Note that
-axis. Note that
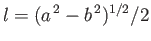 and
and 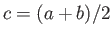 . The corresponding stream function in the
. The corresponding stream function in the  -plane is
-plane is
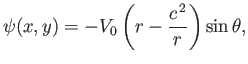 |
(6.75) |
where
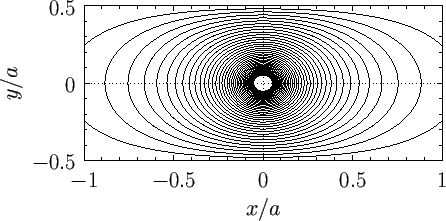
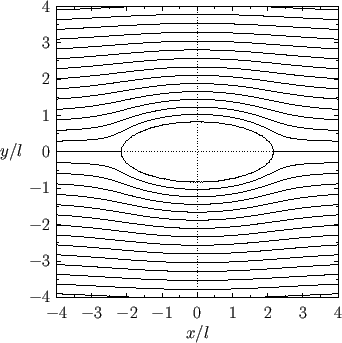
Figure 6.11 shows the streamlines of the flow pattern calculated for  .
.
Figure:
Stream lines of the two-dimensional flow pattern due to uniform flow parallel to the  -axis
around an elliptical cylinder.
-axis
around an elliptical cylinder.
 |



Next: Schwarz-Christoffel Theorem
Up: Two-Dimensional Potential Flow
Previous: Method of Images
Richard Fitzpatrick
2016-03-31
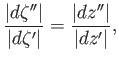
![]() is a well-behaved function of the complex variable
is a well-behaved function of the complex variable ![]() . It follows
that
. It follows
that
![]() . Hence, the functions
. Hence, the functions
![]() and
and
![]() can be interpreted
as the velocity potential and stream function, respectively, of some two-dimensional, incompressible, irrotational flow pattern, where
can be interpreted
as the velocity potential and stream function, respectively, of some two-dimensional, incompressible, irrotational flow pattern, where ![]() and
and
![]() are Cartesian coordinates.
However, if
are Cartesian coordinates.
However, if
![]() , where
, where ![]() is well-behaved, then
is well-behaved, then
![]() , where
, where ![]() is also well-behaved. It follows that
is also well-behaved. It follows that
![]() . In other words, the functions
. In other words, the functions
![]() and
and
![]() can be interpreted
as the velocity potential and stream function, respectively, of some new, two-dimensional, incompressible, irrotational flow pattern, where
can be interpreted
as the velocity potential and stream function, respectively, of some new, two-dimensional, incompressible, irrotational flow pattern, where ![]() and
and
![]() are Cartesian coordinates. In other words, we can use a conformal map to convert a given two-dimensional, incompressible, irrotational flow pattern into another, quite different, pattern.
Incidentally, a conformal map converts a line source into a line source of the same strength, and a vortex filament into a vortex filament of the same intensity. (See Exercise 12.)
are Cartesian coordinates. In other words, we can use a conformal map to convert a given two-dimensional, incompressible, irrotational flow pattern into another, quite different, pattern.
Incidentally, a conformal map converts a line source into a line source of the same strength, and a vortex filament into a vortex filament of the same intensity. (See Exercise 12.)
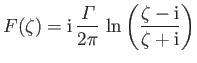
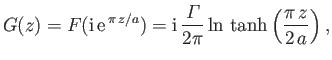
![$\displaystyle \psi(x,y)= \frac{{\mit\Gamma}}{\pi}\,\ln\left[\frac{\cosh(\pi\,x\,a)-\cos(\pi\,y/a) }{\cosh(\pi\,x/a)+\cos(\pi\,y/a)}\right],$](img2109.png)

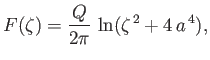
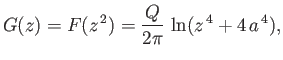
![$\displaystyle \psi(x,y) = -\frac{Q}{2\pi}\,\tan^{-1}\left[\frac{4\,x\,y\,(x^{\,2}-y^{\,2})}{x^{\,4}-6\,x^{\,2}\,y^{\,2}+y^{\,4}+4\,a^{\,4}}\right],$](img2119.png)

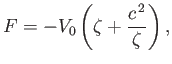
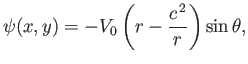
![$\displaystyle = \tan^{-1}\left(\frac{y}{x}\,\frac{p}{[p^{\,2}-1]^{1/2}}\right),$](img2139.png)
![$\displaystyle =\left[\frac{x^{\,2}/l^{\,2}+y^{\,2}/l^{\,2}+4+\left([x^{\,2}/l^{\,2}+y^{\,2}/l^{\,2}+4]^2-16\,x^{\,2}/l^{\,2}\right)^{1/2}}{8}\right]^{1/2}.$](img2141.png)
