


Next: Complex Functions
Up: Two-Dimensional Potential Flow
Previous: Two-Dimensional Potential Flow
This chapter describes the use of complex analysis to facilitate calculations in two-dimensional, incompressible, irrotational
fluid dynamics. Incidentally, incompressible, irrotational flow is usually referred to as potential flow, because the
associated velocity field can be represented in terms of a velocity potential that satisfies Laplace's equation. (See Section 4.15.)
In the following, all flow patterns are assumed to be such that the  -coordinate is ignorable. In other words,
the fluid velocity is everywhere parallel to the
-coordinate is ignorable. In other words,
the fluid velocity is everywhere parallel to the  -
- plane, and
plane, and
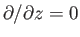 . It follows that all line
sources and vortex filaments run parallel to the
. It follows that all line
sources and vortex filaments run parallel to the  -axis. Moreover, all solid surfaces are of infinite extent in the
-axis. Moreover, all solid surfaces are of infinite extent in the  -direction, and
have uniform cross-sections. Hence, it is only necessary to specify the locations of line sources, vortex filaments, and
solid surfaces in the
-direction, and
have uniform cross-sections. Hence, it is only necessary to specify the locations of line sources, vortex filaments, and
solid surfaces in the  -
- plane. More information on the use of complex analysis in two-dimensional fluid
mechanics can be found in Batchelor 2000, Milne-Thomson 1958, Milne-Thomson 2011, and Lamb 1993.
plane. More information on the use of complex analysis in two-dimensional fluid
mechanics can be found in Batchelor 2000, Milne-Thomson 1958, Milne-Thomson 2011, and Lamb 1993.
Richard Fitzpatrick
2016-03-31