


Next: Surface Tension
Up: Hydrostatics
Previous: Roche Ellipsoids
- A hollow vessel floats in a basin. If, as a consequence of a leak, water flows slowly into the vessel, how
will the level of the water in the basin be affected? (Lamb 1928.)
- A hollow spherical shell made up of material of specific gravity
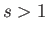 has external and internal
radii
has external and internal
radii  and
and 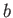 , respectively. Demonstrate that the sphere will only float in water if
, respectively. Demonstrate that the sphere will only float in water if
- Show that the equilibrium of a solid of uniform density floating with an edge or corner just emerging
from the water is unstable. (Lamb 1928.)
- Prove that if a solid of uniform density floats with a flat face just above the waterline then the
equilibrium is stable. (Lamb 1928.)
- Demonstrate that a uniform solid cylinder floating with its axis horizontal is in a stable equilibrium
provided that its length exceeds the breadth of the waterline section. [Hint: The cylinder is obviously neutrally
stable to rotations about its axis, which means that the corresponding metacentric height is zero.] (Lamb 1928.)
- Show that a uniform solid cylinder of radius
 and height
and height 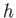 can float in stable equilibrium, with its
axis vertical, if
can float in stable equilibrium, with its
axis vertical, if
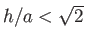 . If the ratio
. If the ratio 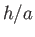 exceeds this value, prove that the equilibrium is
only stable when the specific gravity of the cylinder lies outside the range
exceeds this value, prove that the equilibrium is
only stable when the specific gravity of the cylinder lies outside the range
- A uniform, thin, hollow cylinder of radius
 and height
and height 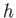 is open at both ends. Assuming that
is open at both ends. Assuming that 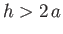 , prove that the
cylinder cannot
float upright if its specific gravity lies in the range
, prove that the
cylinder cannot
float upright if its specific gravity lies in the range
(Lamb 1928.)
- Show that the cylinder of the preceding exercise can float with its axis horizontal provided
where 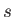 is the specific gravity of the cylinder. (Lamb 1928.)
is the specific gravity of the cylinder. (Lamb 1928.)
- Prove that any segment of a uniform sphere, made up of a substance lighter than water, can float in
stable equilibrium with its plane surface horizontal and immersed. (Lamb 1928.)
- A vessel carries a tank of oil, of specific gravity
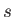 , running along its length. Assuming that the
surface of the oil is at sea level, show that the effect of the oil's fluidity on the rolling of the vessel is equivalent to a reduction in the metacentric height by
, running along its length. Assuming that the
surface of the oil is at sea level, show that the effect of the oil's fluidity on the rolling of the vessel is equivalent to a reduction in the metacentric height by
 ,
where
,
where  is the displacement of the ship,
is the displacement of the ship,  the surface-area of the tank, and
the surface-area of the tank, and 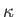 the radius
of gyration of this area. In what ratio is the effect diminished when a longitudinal partition bisects the
tank? (Lamb 1928.)
the radius
of gyration of this area. In what ratio is the effect diminished when a longitudinal partition bisects the
tank? (Lamb 1928.)
- Find the stable equilibrium configurations of a cylinder of elliptic cross-section, with major and minor radii
 and
and
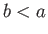 , respectively, made up of material of specific gravity
, respectively, made up of material of specific gravity 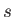 , which floats with its axis horizontal.
, which floats with its axis horizontal.
- A cylindrical tank has a circular cross-section of radius
 .
Let the center of gravity of the tank be located a
distance
.
Let the center of gravity of the tank be located a
distance 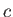 above its base. Suppose that the tank is pivoted about a horizontal axis passing through its
center of gravity, and is then filled with fluid up to a depth
above its base. Suppose that the tank is pivoted about a horizontal axis passing through its
center of gravity, and is then filled with fluid up to a depth 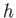 above its base. Demonstrate that the position in which the
tank's axis is upright is unstable for all filling depths provided
above its base. Demonstrate that the position in which the
tank's axis is upright is unstable for all filling depths provided
Show that if
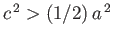 then the upright position is stable when
then the upright position is stable when 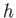 lies in the range
lies in the range
- A thin cylindrical vessel of cross-sectional area
 floats upright, being immersed to a depth
floats upright, being immersed to a depth 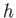 , and
contains water to a depth
, and
contains water to a depth 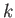 . Show that the work required to pump out the water is
. Show that the work required to pump out the water is
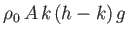 .
(Lamb 1928.)
.
(Lamb 1928.)
- A sphere of radius
 is just immersed in water that is contained in a cylindrical vessel of radius
is just immersed in water that is contained in a cylindrical vessel of radius 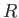 whose
axis is vertical. Prove that if the sphere is raised just clear of the water then the water's loss of potential energy is
whose
axis is vertical. Prove that if the sphere is raised just clear of the water then the water's loss of potential energy is
where 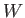 is the weight of the water originally displaced by the sphere. (Lamb 1928.)
is the weight of the water originally displaced by the sphere. (Lamb 1928.)
- A sphere of radius
 , weight
, weight 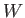 , and specific gravity
, and specific gravity 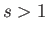 , rests on the bottom of
a cylindrical vessel of radius
, rests on the bottom of
a cylindrical vessel of radius 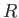 whose axis is vertical, and which contains
water to a depth
whose axis is vertical, and which contains
water to a depth 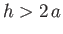 . Show that the work required to lift the sphere out of the
vessel is less than if the water had been absent by an amount
. Show that the work required to lift the sphere out of the
vessel is less than if the water had been absent by an amount
(Lamb 1928.)
- A lead weight is immersed in water that is steadily rotating at an angular velocity
 about a vertical axis, the
weight being suspended from a fixed point on this axis by a string of length
about a vertical axis, the
weight being suspended from a fixed point on this axis by a string of length 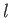 . Prove that the
position in which the weight hangs vertically downward is stable or unstable depending on whether
. Prove that the
position in which the weight hangs vertically downward is stable or unstable depending on whether
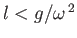 or
or
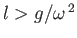 ,
respectively. Also, show that if the vertical position is unstable then there exists a stable inclined position in which the
string is normal to the surface of equal pressure passing though the weight.
,
respectively. Also, show that if the vertical position is unstable then there exists a stable inclined position in which the
string is normal to the surface of equal pressure passing though the weight.
- A thin cylindrical vessel of radius
 and height
and height 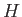 is orientated such that its axis is vertical. Suppose that the
vessel is filled with liquid of density
is orientated such that its axis is vertical. Suppose that the
vessel is filled with liquid of density  to
some height
to
some height  above the base, spun about its axis at a steady angular velocity
above the base, spun about its axis at a steady angular velocity  , and the liquid
allowed to attain a steady state. Demonstrate that, provided
, and the liquid
allowed to attain a steady state. Demonstrate that, provided
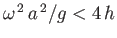 and
and
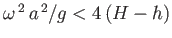 ,
the net radial thrust on the vertical walls of the vessel is
,
the net radial thrust on the vertical walls of the vessel is
- A thin cylindrical vessel of radius
 with a plane horizontal lid is just filled with liquid of density
with a plane horizontal lid is just filled with liquid of density  , and
the whole rotated about a vertical axis at a fixed angular velocity
, and
the whole rotated about a vertical axis at a fixed angular velocity  . Prove that the net upward thrust of the
fluid on the lid is
. Prove that the net upward thrust of the
fluid on the lid is
- A liquid-filled thin spherical vessel of radius
 spins about a vertical diameter at the fixed angular velocity
spins about a vertical diameter at the fixed angular velocity  .
Assuming that the liquid co-rotates with the vessel, and that
.
Assuming that the liquid co-rotates with the vessel, and that
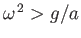 , show that the pressure on the wall of the
vessel is greatest a depth
, show that the pressure on the wall of the
vessel is greatest a depth
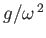 below the center. Also prove that the net normal thrusts on the lower
and upper hemispheres are
below the center. Also prove that the net normal thrusts on the lower
and upper hemispheres are
and
respectively,
where 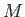 is the mass of the liquid.
is the mass of the liquid.
- A closed cubic vessel filled with water is rotating about a vertical axis passing through the centers of two opposite sides.
Demonstrate that, as a consequence of the rotation, the net thrust on a side is increased by
where  is the length of an edge of the cube, and
is the length of an edge of the cube, and  the angular velocity of rotation.
the angular velocity of rotation.
- A closed vessel filled with water is rotating at constant angular velocity
 about a horizontal axis. Show that,
in the state of relative equilibrium, the constant pressure surfaces in the water are circular cylinders whose common axis
is a height
about a horizontal axis. Show that,
in the state of relative equilibrium, the constant pressure surfaces in the water are circular cylinders whose common axis
is a height
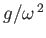 above the axis of rotation. (Batchelor 2000.)
above the axis of rotation. (Batchelor 2000.)
- Verify Equations (2.95)-(2.97) and (2.99)-(2.101).
- Consider a homogeneous, rotating, liquid body of mass
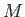 , mean radius
, mean radius 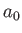 , and angular velocity
, and angular velocity  , whose
outer boundary is a Maclaurin spheroid of eccentricity
, whose
outer boundary is a Maclaurin spheroid of eccentricity 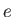 .
.
- Demonstrate that
in the low rotation limit,
 . Hence, show that
. Hence, show that  for the case of a homogeneous body with the
same mass and volume as the Earth,
which rotates once every 24 hours.
for the case of a homogeneous body with the
same mass and volume as the Earth,
which rotates once every 24 hours.
- Show that the critical angular velocity at which the bifurcation to the sequence of Jacobi ellipsoids
takes place is
and occurs when 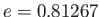 . Hence, show that, for the case of a homogeneous body with the same
mass and volume as the Earth, the bifurcation
would take place at a critical rotation period of
. Hence, show that, for the case of a homogeneous body with the same
mass and volume as the Earth, the bifurcation
would take place at a critical rotation period of
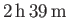 .
.
- Demonstrate that the maximum angular velocity consistent with a spheroidal shape is
and occurs when 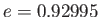 . Hence, show that, for the case of a homogeneous body with the same mass and volume as the Earth, this maximum velocity
corresponds to a minimum rotation period of
. Hence, show that, for the case of a homogeneous body with the same mass and volume as the Earth, this maximum velocity
corresponds to a minimum rotation period of
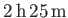 .
.



Next: Surface Tension
Up: Hydrostatics
Previous: Roche Ellipsoids
Richard Fitzpatrick
2016-03-31
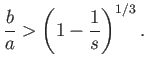
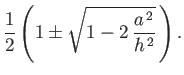
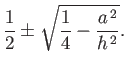
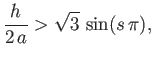
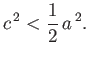

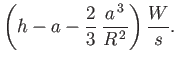
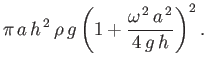

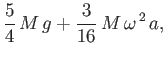
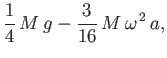
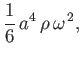
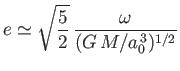
 . Hence, show that
. Hence, show that  for the case of a homogeneous body with the
same mass and volume as the Earth,
which rotates once every 24 hours.
for the case of a homogeneous body with the
same mass and volume as the Earth,
which rotates once every 24 hours.
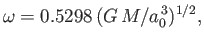
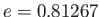 . Hence, show that, for the case of a homogeneous body with the same
mass and volume as the Earth, the bifurcation
would take place at a critical rotation period of
. Hence, show that, for the case of a homogeneous body with the same
mass and volume as the Earth, the bifurcation
would take place at a critical rotation period of
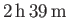 .
.
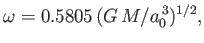
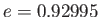 . Hence, show that, for the case of a homogeneous body with the same mass and volume as the Earth, this maximum velocity
corresponds to a minimum rotation period of
. Hence, show that, for the case of a homogeneous body with the same mass and volume as the Earth, this maximum velocity
corresponds to a minimum rotation period of
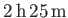 .
.