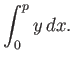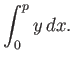Next: Bibliography
Up: Calculus of Variations
Previous: Multi-Function Variation
- Find the extremal curves
 of the following constrained optimization problems, using the method of Lagrange multipliers:
of the following constrained optimization problems, using the method of Lagrange multipliers:
-
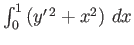 , such that
, such that
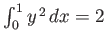 .
.
-
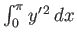 , such that
, such that
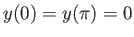 , and
, and
 .
.
-
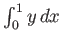 , such that
, such that
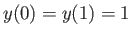 , and
, and
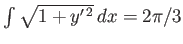 .
.
- Suppose
 and
and  are two points lying in the
are two points lying in the  -
- plane, which is orientated vertically such that
plane, which is orientated vertically such that  is above
is above  . Imagine there is a thin, flexible wire connecting the two points and lying entirely in the
. Imagine there is a thin, flexible wire connecting the two points and lying entirely in the  -
- plane. A frictionless bead travels down the wire, impelled by gravity alone. Show that the shape of the wire that results in the bead reaching the point
plane. A frictionless bead travels down the wire, impelled by gravity alone. Show that the shape of the wire that results in the bead reaching the point  in the least amount of time is a cycloid, which takes the parametric form
in the least amount of time is a cycloid, which takes the parametric form
where 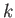 is a constant.
is a constant.
- Find the curve
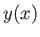 , in the interval
, in the interval
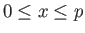 , which is of length
, which is of length 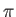 , and maximizes
, and maximizes



Next: Bibliography
Up: Calculus of Variations
Previous: Multi-Function Variation
Richard Fitzpatrick
2016-03-31
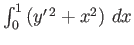 , such that
, such that
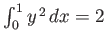 .
.
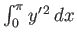 , such that
, such that
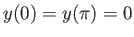 , and
, and
 .
.
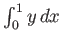 , such that
, such that
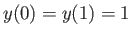 , and
, and
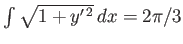 .
.