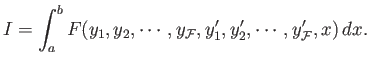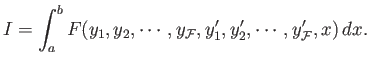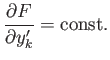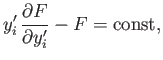

Next: Exercises
Up: Calculus of Variations
Previous: Conditional Variation
Multi-Function Variation
Suppose that we wish to maximize or minimize the functional
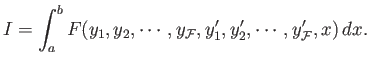 |
(E.33) |
Here, the integrand 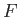 is now a functional of the
is now a functional of the 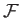 independent
functions
independent
functions 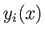 , for
, for
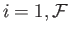 . A fairly straightforward extension of the
analysis in Section E.2 yields
. A fairly straightforward extension of the
analysis in Section E.2 yields 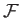 separate Euler-Lagrange equations,
separate Euler-Lagrange equations,
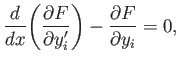 |
(E.34) |
for
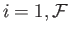 , which determine the
, which determine the 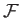 functions
functions 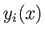 . If
. If 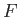 does not
explicitly depend on the function
does not
explicitly depend on the function 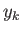 then the
then the 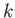 th Euler-Lagrange
equation simplifies to
th Euler-Lagrange
equation simplifies to
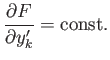 |
(E.35) |
Likewise, if 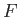 does not explicitly depend on
does not explicitly depend on 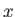 then all
then all 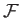 Euler-Lagrange equations simplify to
Euler-Lagrange equations simplify to
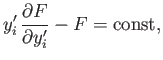 |
(E.36) |
for
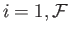 .
.
Richard Fitzpatrick
2016-03-31