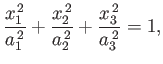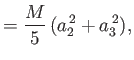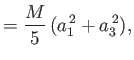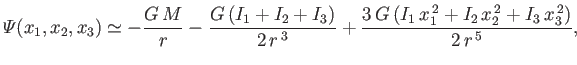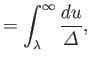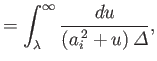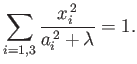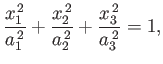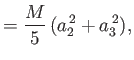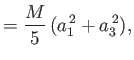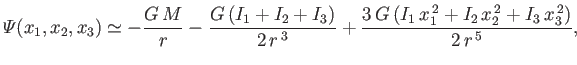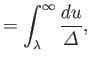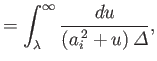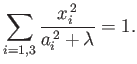Next: Calculus of Variations
Up: Ellipsoidal Potential Theory
Previous: Analysis
- Demonstrate that the volume of an ellipsoid whose bounding surface satisfies
is
 .
.
- Demonstrate that the moments of inertia about the three Cartesian axes of a homogeneous ellipsoidal body of mass
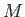 ,
whose bounding surface satisfies
,
whose bounding surface satisfies
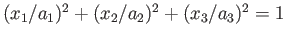 ,
are
,
are
- According to MacCullagh's formula (Fitzpatrick 2012), the gravitational potential a relatively long
way from a body of mass
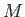 whose center of mass coincides with the origin, and whose principal moments of inertial are
whose center of mass coincides with the origin, and whose principal moments of inertial are 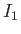 ,
, 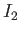 , and
, and 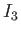 (assuming that
the principal axes coincide with the Cartesian axes), takes the form
(assuming that
the principal axes coincide with the Cartesian axes), takes the form
where
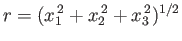 . Demonstrate that if the body in question is a homogeneous
ellipsoid whose bounding surface satisfies
. Demonstrate that if the body in question is a homogeneous
ellipsoid whose bounding surface satisfies
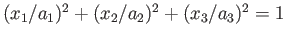 then
then
- Show that the gravitational potential external to a homogeneous ellipsoidal body of mass
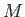 ,
whose outer boundary satisfies
,
whose outer boundary satisfies
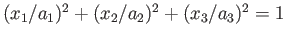 , takes the form
, takes the form
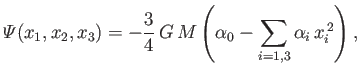 |
(D.38) |
where
and
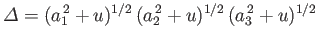 .
Here,
.
Here, 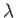 is the positive root of
is the positive root of
Demonstrate that, at large 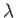 , Equation (D.38) reduces to Equation (D.37).
, Equation (D.38) reduces to Equation (D.37).



Next: Calculus of Variations
Up: Ellipsoidal Potential Theory
Previous: Analysis
Richard Fitzpatrick
2016-03-31