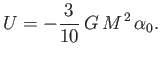Next: Exercises
Up: Ellipsoidal Potential Theory
Previous: Introduction
Consider the contribution to the potential at  from the mass contained within a double cone, whose apex
is
from the mass contained within a double cone, whose apex
is  , and which is terminated in both directions at the body's outer boundary. (See Figure D.1.)
If the cone subtends a solid angle
, and which is terminated in both directions at the body's outer boundary. (See Figure D.1.)
If the cone subtends a solid angle
 then a volume element is written
then a volume element is written
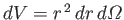 , where
, where
 measures displacement from
measures displacement from 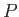 along the axis of the cone. Thus, from standard classical gravitational theory (Fitzpatrick 2012), the
contribution to the potential takes the form
along the axis of the cone. Thus, from standard classical gravitational theory (Fitzpatrick 2012), the
contribution to the potential takes the form
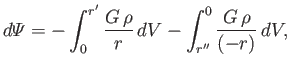 |
(D.2) |
where 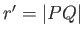 ,
, 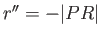 , and
, and  is the constant mass density of the ellipsoid. Hence, we obtain
is the constant mass density of the ellipsoid. Hence, we obtain
 |
(D.3) |
The net potential at 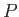 is obtained by integrating over all solid angle, and dividing the result by two to adjust for
double counting. This yields
is obtained by integrating over all solid angle, and dividing the result by two to adjust for
double counting. This yields
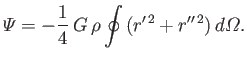 |
(D.4) |
Figure D.1:
Calculation of ellipsoidal gravitational potential.
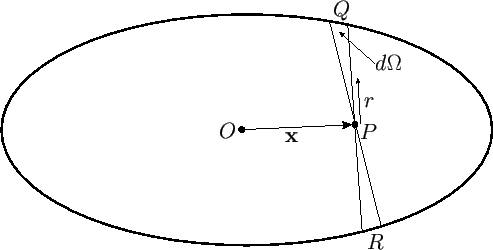 |
From Figure D.1, the position vector of point  , relative to the origin,
, relative to the origin, 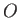 , is
, is
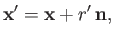 |
(D.5) |
where
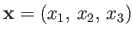 is the position vector of point
is the position vector of point 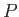 , and
, and 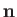 a unit vector pointing from
a unit vector pointing from 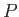 to
to  . Likewise, the position vector of point
. Likewise, the position vector of point 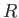 is
is
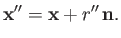 |
(D.6) |
However,  and
and 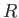 both lie on the body's outer boundary. It follows, from Equation (D.1), that
both lie on the body's outer boundary. It follows, from Equation (D.1), that  and
and 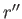 are
the two roots of
are
the two roots of
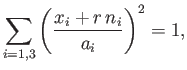 |
(D.7) |
which reduces to the quadratic
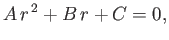 |
(D.8) |
where
According to standard polynomial equation theory (Riley 1974),
 , and
, and
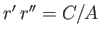 . Thus,
. Thus,
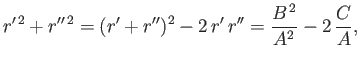 |
(D.12) |
and Equation (D.4) becomes
![$\displaystyle {\mit\Psi} = -\frac{1}{2}\,G\,\rho\oint\left[ \frac{2\left(\sum_{...
...,3}x_i^{\,2}/a_i^{\,2}}{\sum_{i=1,3}n_i^{\,2}/a_i^{\,2}} \right] d{\mit\Omega}.$](img7249.png) |
(D.13) |
The previous expression can also be written
![$\displaystyle {\mit\Psi} = -\frac{1}{2}\,G\,\rho\oint\left[ \frac{2\sum_{i,j=1,...
...,3}x_i^{\,2}/a_i^{\,2}}{\sum_{i=1,3}n_i^{\,2}/a_i^{\,2}} \right] d{\mit\Omega}.$](img7250.png) |
(D.14) |
However, the cross terms (i.e., 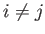 ) integrate to zero by symmetry, and we are left with
) integrate to zero by symmetry, and we are left with
![$\displaystyle {\mit\Psi} = -\frac{1}{2}\,G\,\rho\oint\left[ \frac{2\sum_{i=1,3}...
...,3}x_i^{\,2}/a_i^{\,2}}{\sum_{i=1,3}n_i^{\,2}/a_i^{\,2}} \right] d{\mit\Omega}.$](img7252.png) |
(D.15) |
Let
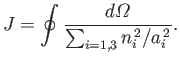 |
(D.16) |
It follows that
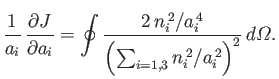 |
(D.17) |
Thus, Equation (D.15) can be written
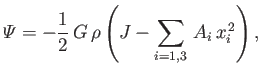 |
(D.18) |
where
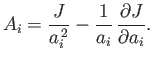 |
(D.19) |
At this stage, it is convenient to adopt the spherical angular coordinates,  and
and 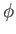 (see Section C.4), in terms of which
(see Section C.4), in terms of which
 |
(D.20) |
and
 . We find, from Equation (D.16), that
. We find, from Equation (D.16), that
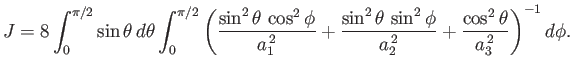 |
(D.21) |
Let
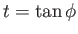 . It follows that
. It follows that
 |
(D.22) |
where
Hence, we obtain
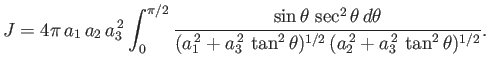 |
(D.25) |
Let
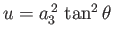 . It follows that
. It follows that
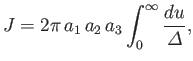 |
(D.26) |
where
 |
(D.27) |
Now, from Equations (D.19), (D.26), and (D.27),
Thus, Equations (D.18), (D.26), and (D.28) yield
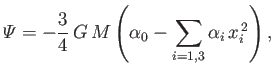 |
(D.29) |
where
Here,
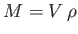 and
and
 are the body's mass and volume, respectively.
are the body's mass and volume, respectively.
The total gravitational potential energy of the body is written (Fitzpatrick 2012)
 |
(D.32) |
where the integral is taken over all interior points. It follows from Equation (D.29) that
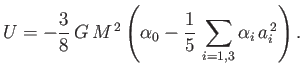 |
(D.33) |
In writing the previous expression, use has been made of the easily demonstrated result
 .
Now,
.
Now,
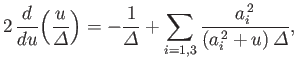 |
(D.34) |
so
![$\displaystyle \sum_{i=1,3}\alpha_i\,a_i^{\,2} = \int_0^\infty \sum_{i=1,3}\frac...
...u}\!\left(\frac{u}{\mit\Delta}\right)+\frac{1}{\mit\Delta}\right]du = \alpha_0.$](img7277.png) |
(D.35) |
Hence, we obtain
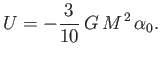 |
(D.36) |



Next: Exercises
Up: Ellipsoidal Potential Theory
Previous: Introduction
Richard Fitzpatrick
2016-03-31
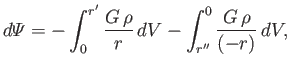
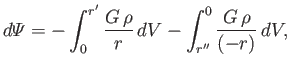
![]() , relative to the origin,
, relative to the origin, ![]() , is
, is
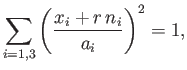
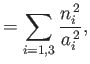
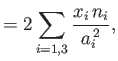
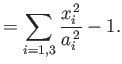
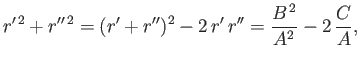
![$\displaystyle {\mit\Psi} = -\frac{1}{2}\,G\,\rho\oint\left[ \frac{2\left(\sum_{...
...,3}x_i^{\,2}/a_i^{\,2}}{\sum_{i=1,3}n_i^{\,2}/a_i^{\,2}} \right] d{\mit\Omega}.$](img7249.png)
![$\displaystyle {\mit\Psi} = -\frac{1}{2}\,G\,\rho\oint\left[ \frac{2\sum_{i,j=1,...
...,3}x_i^{\,2}/a_i^{\,2}}{\sum_{i=1,3}n_i^{\,2}/a_i^{\,2}} \right] d{\mit\Omega}.$](img7250.png)
![]() and
and ![]() (see Section C.4), in terms of which
(see Section C.4), in terms of which

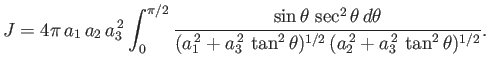

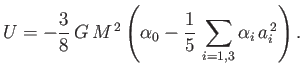
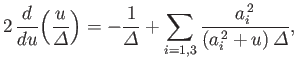
![$\displaystyle \sum_{i=1,3}\alpha_i\,a_i^{\,2} = \int_0^\infty \sum_{i=1,3}\frac...
...u}\!\left(\frac{u}{\mit\Delta}\right)+\frac{1}{\mit\Delta}\right]du = \alpha_0.$](img7277.png)