


Next: Buoyancy
Up: Hydrostatics
Previous: Introduction
Hydrostatic Pressure
Consider a body of water which is stationary in a reference frame that is fixed with respect to the Earth's surface. In this chapter, such a frame is
treated as approximately inertial. Let  measure vertical height, and suppose that the region
measure vertical height, and suppose that the region 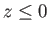 is occupied
by water, and the region
is occupied
by water, and the region  by air.
According to Equation (1.79), the air/water system remains in mechanical equilibrium (i.e.,
by air.
According to Equation (1.79), the air/water system remains in mechanical equilibrium (i.e.,
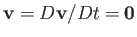 ) provided
) provided
 |
(2.1) |
where  is the static fluid pressure,
is the static fluid pressure,  the mass density,
the mass density,
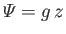 the gravitational potential energy per unit mass, and
the gravitational potential energy per unit mass, and 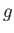 the (approximately uniform) acceleration due to gravity.
Now,
the (approximately uniform) acceleration due to gravity.
Now,
![$\displaystyle \rho(z) = \left\{ \begin{array}{ccc} 0&\mbox{\hspace{0.5cm}}&z>0\\ [0.5ex] \rho_0&&z\leq 0 \end{array}\right.,$](img561.png) |
(2.2) |
where 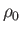 is the (approximately uniform) mass density of water. Here, the comparatively small mass density of air has been neglected. Because
is the (approximately uniform) mass density of water. Here, the comparatively small mass density of air has been neglected. Because
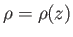 and
and
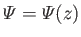 , it immediately follows, from Equation (2.1), that
, it immediately follows, from Equation (2.1), that  ,
where
,
where
 |
(2.3) |
We conclude that constant pressure
surfaces in a stationary body of water take the form of horizontal planes.
Making use of Equation (2.2), the previous equation can be integrated to give
![$\displaystyle p(z)=\left\{\begin{array}{llc} p_0&\mbox{\hspace{1cm}}&z>0\\ [0.5ex] p_0-\rho_0\,g\,z&&z\leq 0 \end{array}\right.,$](img566.png) |
(2.4) |
where
 is atmospheric pressure at ground level (Batchelor 2000). According to this expression, pressure in stationary water increases linearly with increasing depth (i.e., with decreasing
is atmospheric pressure at ground level (Batchelor 2000). According to this expression, pressure in stationary water increases linearly with increasing depth (i.e., with decreasing  , for
, for 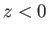 ).
In fact, given that
).
In fact, given that
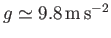 and
and
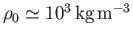 (Batchelor 2000), we deduce that
hydrostatic pressure in water rises
at the rate of 1 atmosphere (i.e.,
(Batchelor 2000), we deduce that
hydrostatic pressure in water rises
at the rate of 1 atmosphere (i.e.,
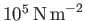 ) every
) every
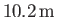 increase in depth below the
surface.
increase in depth below the
surface.



Next: Buoyancy
Up: Hydrostatics
Previous: Introduction
Richard Fitzpatrick
2016-03-31