


Next: Scalar Product
Up: Vectors and Vector Fields
Previous: Cartesian Components of a
Coordinate Transformations
A Cartesian coordinate system allows position and direction in space to be represented in a very convenient
manner. Unfortunately, such a coordinate system also introduces arbitrary elements into our analysis. After all, two independent observers might well choose Cartesian coordinate systems with different origins, and
different orientations of the coordinate axes. In general, a given vector  will have different
sets of components in these two coordinate systems. However, the direction and magnitude of
will have different
sets of components in these two coordinate systems. However, the direction and magnitude of  are the
same in both cases. Hence, the two sets of components must be related to one another in a very particular fashion.
Actually, because vectors are represented by moveable line elements in space (i.e., in Figure A.2,
are the
same in both cases. Hence, the two sets of components must be related to one another in a very particular fashion.
Actually, because vectors are represented by moveable line elements in space (i.e., in Figure A.2,
 and
and
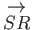 represent the same vector), it follows that
the components of a general vector are not affected by a simple shift in the origin of a Cartesian coordinate system. On the other hand, the
components are modified when the coordinate axes are rotated.
represent the same vector), it follows that
the components of a general vector are not affected by a simple shift in the origin of a Cartesian coordinate system. On the other hand, the
components are modified when the coordinate axes are rotated.
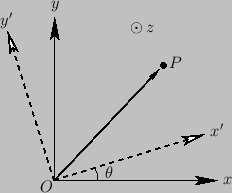
Suppose that we transform to a new coordinate system,  , which has the
same origin as
, which has the
same origin as 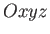 , and is obtained by
rotating the coordinate axes of
, and is obtained by
rotating the coordinate axes of 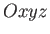 through an angle
through an angle
 about
about 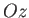 . (See Figure A.5.)
Let the coordinates of a general point
. (See Figure A.5.)
Let the coordinates of a general point 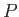 be
be
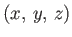 in
in 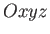 and
and
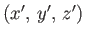 in
in  . According to simple trigonometry, these two sets of coordinates are related to one another via the transformation
. According to simple trigonometry, these two sets of coordinates are related to one another via the transformation
Consider the vector displacement
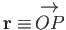 .
Note that this displacement is represented by the same symbol,
.
Note that this displacement is represented by the same symbol,  , in both
coordinate systems, because the magnitude and
direction of
, in both
coordinate systems, because the magnitude and
direction of  are manifestly independent of the orientation of the coordinate axes. The
coordinates of
are manifestly independent of the orientation of the coordinate axes. The
coordinates of  do depend on the orientation of the axes: that is,
do depend on the orientation of the axes: that is,
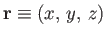 in
in 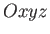 , and
, and
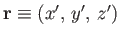 in
in  .
However, they must depend in a very specific manner [i.e., Equations (A.17)-(A.19)] which
preserves the magnitude and direction of
.
However, they must depend in a very specific manner [i.e., Equations (A.17)-(A.19)] which
preserves the magnitude and direction of  .
.
Figure:
Rotation of the coordinate axes about  .
.
 |
The
components of a general vector  transform in an analogous
manner to Equations (A.17)-(A.19): that is,
transform in an analogous
manner to Equations (A.17)-(A.19): that is,
Moreover, there are similar transformation rules for rotation about  and
and  .
Equations (A.20)-(A.22) effectively constitute the definition of a vector: in other words,
the three
quantities (
.
Equations (A.20)-(A.22) effectively constitute the definition of a vector: in other words,
the three
quantities (
 ) are the components of a vector provided that
they transform under rotation of the coordinate axes about
) are the components of a vector provided that
they transform under rotation of the coordinate axes about 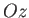 in accordance with Equations (A.20)-(A.22). (And also transform
correctly under rotation about
in accordance with Equations (A.20)-(A.22). (And also transform
correctly under rotation about 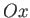 and
and  .)
Conversely, (
.)
Conversely, (
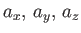 ) cannot be the components of a vector if they
do not transform in accordance with Equations (A.20)-(A.22). Of course, scalar quantities are invariant
under rotation of the coordinate axes.
Thus, the individual components of a vector (
) cannot be the components of a vector if they
do not transform in accordance with Equations (A.20)-(A.22). Of course, scalar quantities are invariant
under rotation of the coordinate axes.
Thus, the individual components of a vector (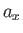 , say) are real numbers, but
they are
not scalars.
Displacement vectors, and all vectors derived from
displacements (e.g., velocity and acceleration), automatically satisfy Equations (A.20)-(A.22). There are, however, other
physical quantities that have both magnitude and direction, but are not
obviously related to displacements. We need to check carefully to see whether these
quantities are really vectors. (See Sections A.7 and A.9.)
, say) are real numbers, but
they are
not scalars.
Displacement vectors, and all vectors derived from
displacements (e.g., velocity and acceleration), automatically satisfy Equations (A.20)-(A.22). There are, however, other
physical quantities that have both magnitude and direction, but are not
obviously related to displacements. We need to check carefully to see whether these
quantities are really vectors. (See Sections A.7 and A.9.)



Next: Scalar Product
Up: Vectors and Vector Fields
Previous: Cartesian Components of a
Richard Fitzpatrick
2016-03-31
![]() , which has the
same origin as
, which has the
same origin as ![]() , and is obtained by
rotating the coordinate axes of
, and is obtained by
rotating the coordinate axes of ![]() through an angle
through an angle
![]() about
about ![]() . (See Figure A.5.)
Let the coordinates of a general point
. (See Figure A.5.)
Let the coordinates of a general point ![]() be
be
![]() in
in ![]() and
and
![]() in
in ![]() . According to simple trigonometry, these two sets of coordinates are related to one another via the transformation
. According to simple trigonometry, these two sets of coordinates are related to one another via the transformation
![]() transform in an analogous
manner to Equations (A.17)-(A.19): that is,
transform in an analogous
manner to Equations (A.17)-(A.19): that is,