Shock-Expansion Theory

It is possible to solve many problems in two-dimensional supersonic flow by patching together appropriate combinations of the oblique shock wave, described in Section 15.2, and the Prandtl-Mayer expansion fan, described in Section 15.6. For example, let us consider the flow over a simple two-dimensional airfoil section.

Figure: A flat lifting plate. ${\rm Ma}_1$ is the upstream Mach number, $p_1$ , $p_2$ , et cetera, denote pressures, and $\alpha _0$ is the angle of attack.

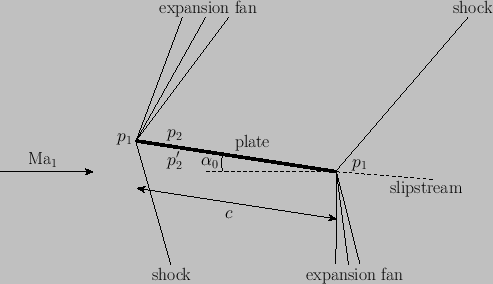
Figure 15.10 shows a flat plate inclined at an angle of attack, $\alpha _0$ , to the oncoming supersonic flow. The streamline ahead of the leading edge is non-inclined, because there is no upstream influence. Moreover, the flow streams over the upper and lower surfaces are completely independent of one another. Thus, the flow on the upper surface is turned through an expansion angle $\alpha _0$ by means of a Prandtl-Mayer expansion fan attached to the leading edge of the airfoil, whereas the flow on the lower side is turned through a compression angle $\alpha _0$ by means of an oblique shock. The flow on the upper surface is recompressed to the upstream pressure $p_1$ by means of an oblique shock wave attached to the trailing edge of the airfoil. Likewise, the flow on the lower surface is re-expanded to the upstream pressure by means of an expansion fan. The uniform pressures, $p_2$ and $p_2'$ , respectively, on the upper and lower surfaces of the airfoil can easily be calculated by means of oblique shock theory and Prandtl-Mayer expansion theory. Given the pressures, the lift and drag per unit transverse length of the airfoil are simply

$$L =(p_2'-p_2)\,c\,\cos\alpha_0,$$ (15.44)

$$D =(p_2'-p_2)\,c\,\sin\alpha_0,$$ (15.45)

respectively, where $c$ is the chord-length (i.e., width). (See Figure 15.10.) The increase in entropy of the flow along the upper surface of the airfoil is not the same as that for the flow along the lower surface, because the upper and lower shock waves occur at different Mach numbers. Consequently, the streamline attached to the trailing edge of the airfoil is a slipstream--that is, it separates flows with the same pressures, but slightly different speeds, temperatures, and densities--inclined at a small angle relative to the free stream. (The angle of inclination is determined by the requirement that the pressures on both sides of the slipstream be equal to one another.)

Note that the drag that develops on the airfoil is of a completely different nature to the previously discussed (see Chapter 9) drags that develop on subsonic airfoils, such as friction drag, form drag, and induced drag. This new type of drag is termed supersonic wave drag, and exists even in an idealized, inviscid fluid. It is ultimately due to the trailing shock waves attached to the airfoil.

Comparatively far from the airfoil, the attached shock waves and expansion fans intersect one another. The expansion fans then attenuate the oblique shocks, making them weak and curved. At very large distances, the shock waves asymptote to free-stream Mach lines. However, this phenomenon does not affect the previous calculation of the lift and drag on a flat-plate airfoil.