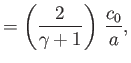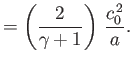Next: Two-Dimensional Compressible Inviscid Flow
Up: One-Dimensional Compressible Inviscid Flow
Previous: Piston-Generated Expansion Wave
- Prove the following useful theorems regarding partial derivatives:
- The specific internal energy of a (not necessarily ideal) gas is defined by
Demonstrate that
and
- The specific enthalpy of a gas is defined by
Demonstrate that
and
- The specific Helmholtz free energy of a gas is defined by
Demonstrate that
and
- The specific Gibbs free energy of a gas is defined by
Demonstrate that
and
- Demonstrate that the specific heat at constant volume of a (not necessarily ideal) gas can be written
Likewise, show that the specific heat at constant pressure takes the form
- The quantities
are known as the coefficient of thermal expansion, the isothermal compressibility, and the
adiabatic compressibility, respectively. Demonstrate that for a (not necessarily ideal) gas,
Hence, deduce that
Show that for the special case of an ideal gas,
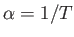 ,
,
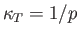 , and
, and
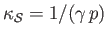 .
Hence, obtain the following standard results for an ideal gas:
.
Hence, obtain the following standard results for an ideal gas:
- Show that for an ideal gas
where 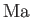 is the Mach number,
is the Mach number, 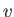 the flow speed, and
the flow speed, and 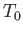 ,
, 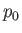 ,
, 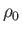 , and
, and 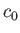 , are the temperature, pressure, density,
and sound speed, respectively, at the stagnation point.
, are the temperature, pressure, density,
and sound speed, respectively, at the stagnation point.
- Consider the flow of an isentropic ideal gas down a straight nozzle with a slowly-varying cross-sectional area,
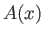 , where
, where
 measures distance along the nozzle. Let
measures distance along the nozzle. Let 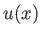 ,
, 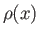 ,
, 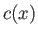 , and
, and
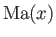 be the flow speed, density, sonic speed, and
Mach number, respectively. Demonstrate that
be the flow speed, density, sonic speed, and
Mach number, respectively. Demonstrate that
and
Hence, show that
Deduce that the throat of the nozzle (where 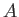 attains its minimum value) either corresponds to
a sonic point (i.e,
attains its minimum value) either corresponds to
a sonic point (i.e,
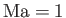 ), or a point of maximum or minimum flow speed.
Finally, demonstrate that
), or a point of maximum or minimum flow speed.
Finally, demonstrate that
Figure 14.4:
A shock tube.
 |
- As indicated in Figure 14.4, a shock tube is a tube of uniform cross section that is divided by a diaphragm into
two chambers that contain different gases at different pressures. Let
 measure distance along the tube, and let the diaphragm be located
at
measure distance along the tube, and let the diaphragm be located
at  . Suppose that the chamber to the left of the diaphragm (which lies at
. Suppose that the chamber to the left of the diaphragm (which lies at 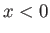 ) is filled with stationary gas of pressure, density, temperature,
and ratio of specific heats,
) is filled with stationary gas of pressure, density, temperature,
and ratio of specific heats, 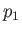 ,
, 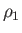 ,
, 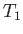 , and
, and 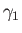 , respectively. Likewise, suppose that the chamber to the right of the diaphragm (which lies at
, respectively. Likewise, suppose that the chamber to the right of the diaphragm (which lies at 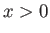 ) is filled with stationary gas of pressure, density, temperature,
and ratio of specific heats,
) is filled with stationary gas of pressure, density, temperature,
and ratio of specific heats,  ,
, 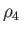 ,
,  , and
, and 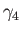 , respectively. It is assumed that
, respectively. It is assumed that 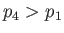 . At
. At  , the diaphragm is ruptured. As indicated in the figure, a shock wave subsequently travels
to the left with speed
, the diaphragm is ruptured. As indicated in the figure, a shock wave subsequently travels
to the left with speed 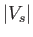 , and an expansion wave to the right with speed
, and an expansion wave to the right with speed 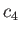 . The so-called contact surface marks the boundary
between the two different gases that were originally on either side of the diaphragm. Neglecting diffusion, the gases do not mix, but are
permanently separated by the contact surface. On either side of the contact surface, which moves to the left with speed
. The so-called contact surface marks the boundary
between the two different gases that were originally on either side of the diaphragm. Neglecting diffusion, the gases do not mix, but are
permanently separated by the contact surface. On either side of the contact surface, which moves to the left with speed 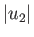 , the
temperatures and densities can be different, but the pressures and flow velocities must be the same. We can
divide the gas in the tube into four regions. Regions 1 lies to the left of the shock wave. Region 2 lies between the shock wave and the
contact surface. Region 3 lies between the contact surface and the expansion wave. Region 4 lies to the right of the expansion wave.
Thus, we expect the flow velocity, pressure, density, temperature, and ratio of heats to be
, the
temperatures and densities can be different, but the pressures and flow velocities must be the same. We can
divide the gas in the tube into four regions. Regions 1 lies to the left of the shock wave. Region 2 lies between the shock wave and the
contact surface. Region 3 lies between the contact surface and the expansion wave. Region 4 lies to the right of the expansion wave.
Thus, we expect the flow velocity, pressure, density, temperature, and ratio of heats to be 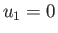 ,
, 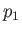 ,
, 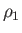 ,
,
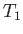 , and
, and 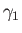 , respectively,
in Region 1;
, respectively,
in Region 1; 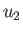 ,
, 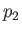 ,
, 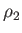 ,
, 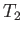 , and
, and 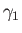 , respectively in Region 2;
, respectively in Region 2; 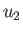 ,
, 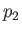 ,
, 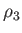 ,
, 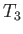 , and
, and 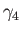 ,
respectively in Region 3; and
,
respectively in Region 3; and  ,
,  ,
, 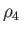 ,
,  , and
, and 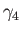 , respectively, in Region 1. Note that
, respectively, in Region 1. Note that 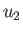 and
and 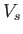 are
negative.
Demonstrate that
are
negative.
Demonstrate that
and
where 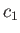 and
and 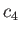 are the sound speeds in Regions 1 and 4, respectively. Hence, obtain
are the sound speeds in Regions 1 and 4, respectively. Hence, obtain
This expression give the shock strength, 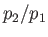 , implicitly as a function of the diaphragm pressure ratio,
, implicitly as a function of the diaphragm pressure ratio, 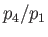 .
All other quantities of interest can be expressed in terms of the shock strength.
Show that
.
All other quantities of interest can be expressed in terms of the shock strength.
Show that
and
- Show that the maximum shock strength and shock speed attainable in a (uniform) shock tube, in the limit
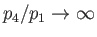 , are
, are
and
respectively. Show, further, that the contact surface moves at the speed
- Show that Equations (14.38) and (14.39) can be written in the form
where 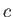 is the sound speed. By adding and subtracting the previous equations, obtain
is the sound speed. By adding and subtracting the previous equations, obtain
These equations indicate that the quantities
 and
and
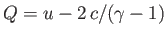 are
constant on curves that have the slope
are
constant on curves that have the slope 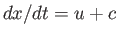 and
and 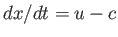 , respectively. These curves are called
characteristics, and
, respectively. These curves are called
characteristics, and  and
and 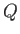 are known as Riemann invariants. In situations in which all the
are known as Riemann invariants. In situations in which all the 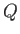 characteristics originate from regions where the gas is at rest, we expect
characteristics originate from regions where the gas is at rest, we expect
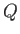 to be constant throughout the gas. Deduce that [cf., Equation (14.50)]
to be constant throughout the gas. Deduce that [cf., Equation (14.50)]
where 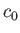 is the stagnation sound speed. Show that
is the stagnation sound speed. Show that
Hence, conclude that the  characteristics are straight-lines.
characteristics are straight-lines.
- Consider a one-dimensional sound wave propagating through an ideal gas whose unperturbed sound speed is
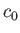 .
At time
.
At time  , the velocity perturbation,
, the velocity perturbation,  , due to the wave, has the form
, due to the wave, has the form
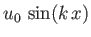 , where
, where
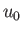 and
and 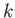 are both positive. Demonstrate that shocks form after a time
are both positive. Demonstrate that shocks form after a time
has elapsed. [Hint: Shocks are associated with the crossing of different  characteristics.] Show that in the time interval
characteristics.] Show that in the time interval  to
to 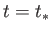 a local maximum of
a local maximum of  travels a
distance
travels a
distance
- An ideal gas is initially at rest in a uniform tube, and occupies the region to the right of a tight-fitting piston whose
position is
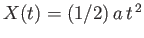 for
for 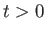 . Here,
. Here, 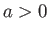 . Show that a shock first forms at
. Show that a shock first forms at 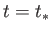 and
and 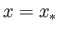 , where
, where
Here, 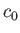 is the stagnation sound speed, and
is the stagnation sound speed, and 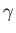 the ratio of specific heats.
the ratio of specific heats.



Next: Two-Dimensional Compressible Inviscid Flow
Up: One-Dimensional Compressible Inviscid Flow
Previous: Piston-Generated Expansion Wave
Richard Fitzpatrick
2016-03-31
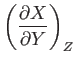
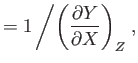
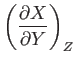
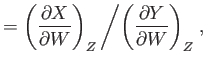
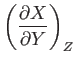
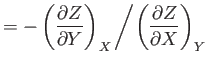
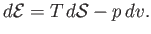
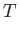
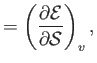
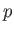
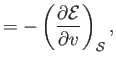
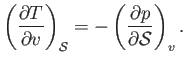
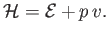
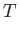
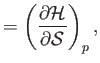
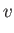
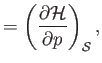

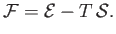

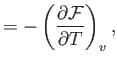
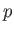

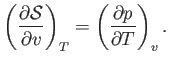
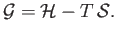

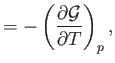
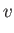
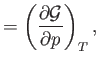

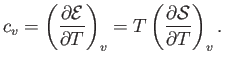

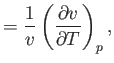

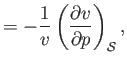
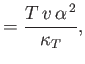
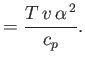
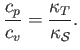

![$\displaystyle = \frac{v}{c_0}\left[1-\frac{1}{2}\,(\gamma-1)\left(\frac{v}{c_0}\right)^2\right]^{\,-1/2},$](img5615.png)
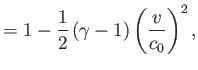
![$\displaystyle = \left[1-\frac{1}{2}\,(\gamma-1)\left(\frac{v}{c_0}\right)^2\right]^{\,\gamma/(\gamma-1)},$](img5618.png)
![$\displaystyle = \left[1-\frac{1}{2}(\gamma-1)\left(\frac{v}{c_0}\right)^2\right]^{\,1/(\gamma-1)},$](img5619.png)
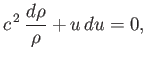
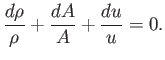

![$\displaystyle \frac{d{\rm Ma}}{{\rm Ma}} = \left[\frac{1+(1/2)\,(\gamma-1)\,{\rm Ma}^{\,2}}{1-{\rm Ma}^{\,2}}\right]\frac{dA}{A}.
$](img5626.png)
![$\displaystyle \vert u_2\vert= c_1\left(\frac{p_2}{p_1}-1\right)\left[\frac{2/\gamma_1}{2\,\gamma_1+ (\gamma_1+1)\,(p_2/p_1-1)}\right]^{\,1/2},
$](img5640.png)
![$\displaystyle \vert u_2\vert = \frac{2\,c_4}{\gamma_4-1}\left[1-\left(\frac{p_2}{p_4}\right)^{(\gamma_4-1)/\gamma_4}\right],
$](img5641.png)
![$\displaystyle \frac{p_4}{p_1}=\frac{p_2}{p_1}\left[1-\frac{(\gamma_4-1)\,(c_1/c...
...t{2\,\gamma_1
+(\gamma_1+1)\,(p_2/p_1-1)}}\right]^{-2\,\gamma_4/(\gamma_4-1)}.
$](img5642.png)
![$\displaystyle = c_1\left[1+\left(\frac{\gamma_1+1}{2\,\gamma_1}\right)\left(\frac{p_2}{p_1}-1\right)\right]^{\,1/2},$](img5646.png)

![$\displaystyle = \frac{p_2}{p_1}\left[\frac{2\,\gamma_1+(\gamma_1-1)\,(p_2/p_1-1)}{2\,\gamma_1+(\gamma_1+1)\,(p_2/p_1-1)}\right],$](img5648.png)
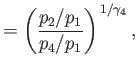
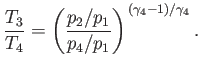
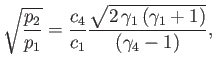
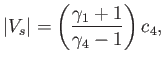

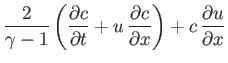
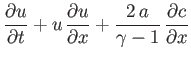
![$\displaystyle \left[\frac{\partial}{\partial t} + (u+c)\,\frac{\partial}{\partial x}\right]\left(u+\frac{2\,c}{\gamma-1}\right)$](img5658.png)
![$\displaystyle \left[\frac{\partial}{\partial t} + (u-c)\,\frac{\partial}{\partial x}\right]\left(u-\frac{2\,c}{\gamma-1}\right)$](img5659.png)

 = 0.
$](img5665.png)
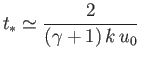
![$\displaystyle \left[1+\frac{2\,c_0}{(\gamma+1)\,u_0}\right]\frac{1}{k},
$](img5670.png)