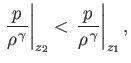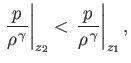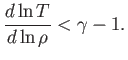Next: Eddington Solar Model
Up: Equilibrium of Compressible Fluids
Previous: Adiabatic Atmosphere
Suppose that the atmosphere is static (i.e., non-convecting). Moreover, let 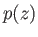 and
and 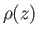 be the pressure and density, respectively, as functions of altitude. Consider a packet of air that is in equilibrium with the surrounding air at some initial altitude
be the pressure and density, respectively, as functions of altitude. Consider a packet of air that is in equilibrium with the surrounding air at some initial altitude 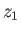 , but subsequently moves to a higher altitude
, but subsequently moves to a higher altitude  .
Thus, the packet's initial pressure and density are
.
Thus, the packet's initial pressure and density are
 and
and
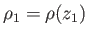 , respectively.
Now, at the higher altitude, the packet must adjust its volume in such a manner that its pressure matches that
of the surrounding air, otherwise there would be a force imbalance across the packet boundary.
It follows that the packet pressure at altitude
, respectively.
Now, at the higher altitude, the packet must adjust its volume in such a manner that its pressure matches that
of the surrounding air, otherwise there would be a force imbalance across the packet boundary.
It follows that the packet pressure at altitude  is
is
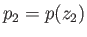 . Assuming that the packet moves upward on a much faster time scale
than that required for heat to diffuse across it (but still a sufficiently slow time scale that it remains in approximate pressure balance with the surrounding air), we would expect its internal pressure and density to be related according to the
adiabatic gas law, (13.4). Thus, the packet's density at altitude
. Assuming that the packet moves upward on a much faster time scale
than that required for heat to diffuse across it (but still a sufficiently slow time scale that it remains in approximate pressure balance with the surrounding air), we would expect its internal pressure and density to be related according to the
adiabatic gas law, (13.4). Thus, the packet's density at altitude  is
is
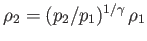 . Now, if
. Now, if
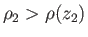 then the packet is denser than the surrounding air. It follows that the
packet's weight exceeds the buoyancy due to the atmosphere, causing the packet to sink back to
its original altitude. On the other hand, if
then the packet is denser than the surrounding air. It follows that the
packet's weight exceeds the buoyancy due to the atmosphere, causing the packet to sink back to
its original altitude. On the other hand, if
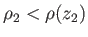 then the packet is less dense than the
surrounding air. It follows that the
buoyancy force exceeds the packet's weight, causing it to rise to an even higher altitude. In other words, the
atmosphere is unstable to vertical convection when
then the packet is less dense than the
surrounding air. It follows that the
buoyancy force exceeds the packet's weight, causing it to rise to an even higher altitude. In other words, the
atmosphere is unstable to vertical convection when
![$ [p(z_2)/p(z_1)]^{1/\gamma}\,\rho(z_1) < \rho(z_2)$](img5166.png) for any
for any
 : that is, when
: that is, when
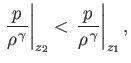 |
(13.18) |
for any  . It follows that the atmosphere is only stable to vertical convection when
. It follows that the atmosphere is only stable to vertical convection when
 is
a monotonically increasing function of altitude. As is easily demonstrated, this stability criterion can also be written
is
a monotonically increasing function of altitude. As is easily demonstrated, this stability criterion can also be written
 |
(13.19) |
or, making use of the ideal gas equation of state,
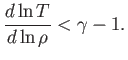 |
(13.20) |
Convection is triggered in regions of the atmosphere where the previous stability criterion is violated. However, such convection acts to relax these
regions back to a marginally-stable state in which
 is uniform: in other words, an adiabatic
equilibrium.
is uniform: in other words, an adiabatic
equilibrium.



Next: Eddington Solar Model
Up: Equilibrium of Compressible Fluids
Previous: Adiabatic Atmosphere
Richard Fitzpatrick
2016-03-31