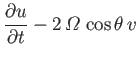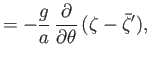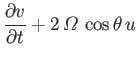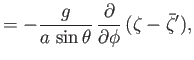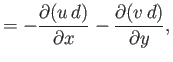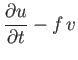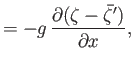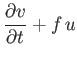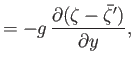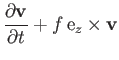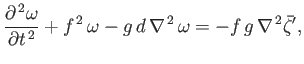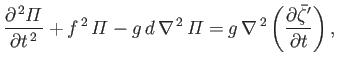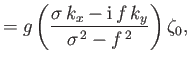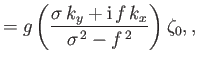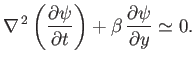Next: Equilibrium of Compressible Fluids
Up: Terrestrial Ocean Tides
Previous: Hemispherical Ocean Tides
- Consider a tidal wave whose wavelength is very much less than the radius of the Earth. This corresponds to the limit
 , where
, where
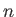 is an azimuthal mode number. Suppose, however, that the ocean depth,
is an azimuthal mode number. Suppose, however, that the ocean depth,  , is allowed to vary with position. Show that, in this limit, the Laplace tidal equations
are written
, is allowed to vary with position. Show that, in this limit, the Laplace tidal equations
are written
where
- Consider short-wavelength tidal waves in a region of the ocean that is sufficiently localized that it is a good approximation to treat
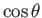 and
and
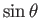 as constants. We can define local Cartesian coordinates,
as constants. We can define local Cartesian coordinates,  ,
,  ,
,  , such that
, such that
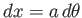 ,
,
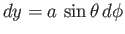 ,
and
,
and 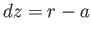 . It follows that the
. It follows that the  -axis is directed southward, the
-axis is directed southward, the  -axis is directed eastward, and the
-axis is directed eastward, and the
 -axis is directed vertically upward. Show that, when expressed in terms of this local coordinate system, the Laplace
tidal equations derived in the previous exercise reduce to
-axis is directed vertically upward. Show that, when expressed in terms of this local coordinate system, the Laplace
tidal equations derived in the previous exercise reduce to
where
is a constant. In fact, the previous equations are the linearized equations of motion of a body of shallow
water confined to a tangent plane that touches the Earth at the angular coordinates  ,
, 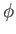 . This
plane is known as the
. This
plane is known as the 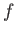 -plane because, as a consequence of the Earth's diurnal rotation, it rotates about
-plane because, as a consequence of the Earth's diurnal rotation, it rotates about
 at the angular velocity
at the angular velocity 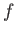 .
.
- Demonstrate that the set of equations derived in the previous exercise can be written in the coordinate-free (in the
 -
- plane) form
plane) form
where
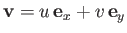 .
Let
.
Let
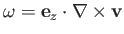 and
and
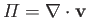 . Assuming that
. Assuming that  and
and 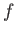 are constants,
demonstrate that the previous equations are equivalent to
are constants,
demonstrate that the previous equations are equivalent to
where
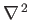 denotes a two-dimensional Laplacian (in the
denotes a two-dimensional Laplacian (in the  -
- plane).
plane).
- Consider free (i.e.,
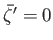 ) plane-wave solutions to the
) plane-wave solutions to the 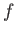 -plane equations, derived in Exercise ii, of the form
-plane equations, derived in Exercise ii, of the form
Here,
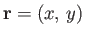 , and
, and 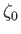 ,
,  ,
, 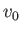 are constants. Assuming that
are constants. Assuming that  is
constant, show that
is
constant, show that
and
where
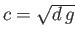 . This type of wave is known as a Poincaré wave.
. This type of wave is known as a Poincaré wave.
- Suppose that the region
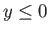 corresponds to an ocean of constant depth
corresponds to an ocean of constant depth  , whereas the region
, whereas the region
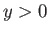 corresponds to land. Consider free solutions to the
corresponds to land. Consider free solutions to the 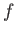 -plane equations in the region
-plane equations in the region 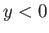 . We
can trivially satisfy the constraint
. We
can trivially satisfy the constraint
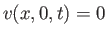 by searching for solutions which are such that
by searching for solutions which are such that  for all
for all 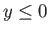 . Show that the most general such solution takes the form
. Show that the most general such solution takes the form
where
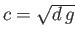 , and
, and
Here,  and
and 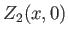 are arbitrary functions,
are arbitrary functions,
 , and
, and
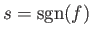 .
These solutions are known as Kelvin waves. Deduce that Kelvin waves propagate
along coastlines, at the speed
.
These solutions are known as Kelvin waves. Deduce that Kelvin waves propagate
along coastlines, at the speed 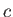 , in such a manner as to keep the coastline to the right of the direction of propagation in the Earth's northern hemisphere, and to
the left in the southern hemisphere.
, in such a manner as to keep the coastline to the right of the direction of propagation in the Earth's northern hemisphere, and to
the left in the southern hemisphere.
- We can take into account the latitude dependence of the parameter
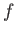 by writing
by writing
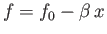 , where
, where
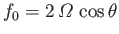 and
and
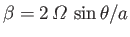 .
Let us assume that the ocean is of constant depth,
.
Let us assume that the ocean is of constant depth,  . Furthermore, let us search for an almost incompressible, free
solution of the Laplace tidal equations which is such that
. Furthermore, let us search for an almost incompressible, free
solution of the Laplace tidal equations which is such that
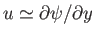 and
and
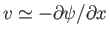 . By eliminating
. By eliminating 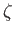 from the final two
from the final two 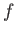 -plane equations,
show that
-plane equations,
show that
By searching for a wavelike solution of the previous equation of the form
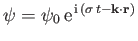 ,
deduce that
,
deduce that
This is the dispersion relation of a so-called Rossby wave. Demonstrate that Rossby waves always travel with a
westward component of phase velocity. Finally, show that it is reasonable to neglect compression provided that
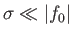 .
.



Next: Equilibrium of Compressible Fluids
Up: Terrestrial Ocean Tides
Previous: Hemispherical Ocean Tides
Richard Fitzpatrick
2016-03-31
![$\displaystyle = - \frac{1}{a\,\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,u\,d)+\frac{\partial (v\,d)}{\partial\phi}\right],$](img5053.png)