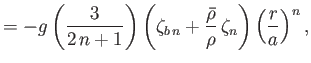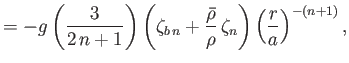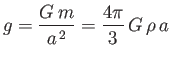

Next: Planetary Response
Up: Terrestrial Ocean Tides
Previous: Planetary Rotation
The planet is modeled as a solid body of uniform mass density 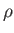 whose surface lies at
whose surface lies at
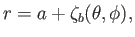 |
(12.45) |
where
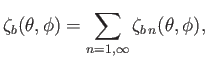 |
(12.46) |
and
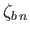 is a surface harmonic of degree
is a surface harmonic of degree 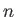 .
Suppose that the planetary surface is covered by an ocean of uniform mass density
.
Suppose that the planetary surface is covered by an ocean of uniform mass density
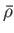 whose surface lies at
whose surface lies at
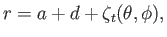 |
(12.47) |
where
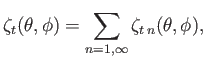 |
(12.48) |
and
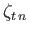 is a surface harmonic of degree
is a surface harmonic of degree 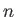 .
Here,
.
Here, 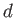 is the constant unperturbed depth of the ocean, whereas
is the constant unperturbed depth of the ocean, whereas 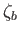 and
and 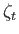 are the radial displacements
of the ocean's bottom and top surfaces, respectively, generated by planetary rotation and tidal effects.
It is assumed that
are the radial displacements
of the ocean's bottom and top surfaces, respectively, generated by planetary rotation and tidal effects.
It is assumed that 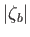 ,
,
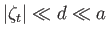 .
.
The net gravitational acceleration in the vicinity of the planet takes the form
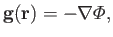 |
(12.49) |
where
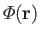 is the total gravitational potential.
In the limit
is the total gravitational potential.
In the limit 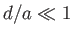 , we can write
, we can write
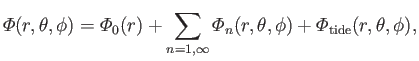 |
(12.50) |
where
![$\displaystyle \nabla^{\,2}{\mit\Phi}_0 =\left\{ \begin{array}{lll} 4\pi\,G\,\rh...
...,\delta(r-a)&\mbox{\hspace{0.5cm}}&r\leq a\\ [0.5ex] 0&&r>a \end{array}\right.,$](img4355.png) |
(12.51) |
and
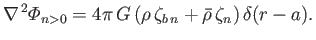 |
(12.52) |
Here,
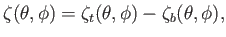 |
(12.53) |
is the net change in ocean depth due to planetary rotation and tidal effects, and
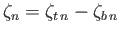 .
Moreover,
.
Moreover, 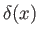 is a Dirac delta function (Riley 1974).
The boundary conditions are that the
is a Dirac delta function (Riley 1974).
The boundary conditions are that the
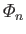 be well behaved as
be well behaved as
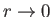 , and
, and
![$\displaystyle {\mit\Phi}_n({\bf r})\rightarrow 0\\ [0.5ex]$](img4360.png) |
(12.54) |
as
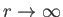 .
It follows that
.
It follows that
and
where
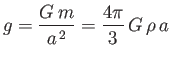 |
(12.59) |
is the mean gravitational acceleration at the planet's surface.
Note that, inside the planet (i.e., 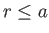 ),
),
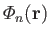 is a solid harmonic of degree
is a solid harmonic of degree 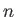 . We can identify the three terms appearing on the right-hand side of Equation (12.50) as
the equilibrium gravitational potential generated by the planet and the ocean, the potential generated by non-spherically-symmetric radial displacements of the planet and ocean surfaces, and the tide generating potential, respectively.
. We can identify the three terms appearing on the right-hand side of Equation (12.50) as
the equilibrium gravitational potential generated by the planet and the ocean, the potential generated by non-spherically-symmetric radial displacements of the planet and ocean surfaces, and the tide generating potential, respectively.


Next: Planetary Response
Up: Terrestrial Ocean Tides
Previous: Planetary Rotation
Richard Fitzpatrick
2016-03-31
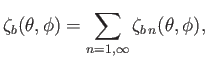
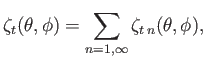
![$\displaystyle \nabla^{\,2}{\mit\Phi}_0 =\left\{ \begin{array}{lll} 4\pi\,G\,\rh...
...,\delta(r-a)&\mbox{\hspace{0.5cm}}&r\leq a\\ [0.5ex] 0&&r>a \end{array}\right.,$](img4355.png)