


Next: Energy of Gravity Waves
Up: Waves in Incompressible Fluids
Previous: Gravity Waves in Deep
Gravity Waves in Shallow Water
Consider the so-called shallow water limit,
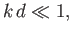 |
(11.35) |
in which the depth, 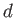 , of the water is much less than the wavelength,
, of the water is much less than the wavelength,
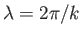 , of the wave.
In this limit, the gravity wave dispersion relation (11.21) reduces to
, of the wave.
In this limit, the gravity wave dispersion relation (11.21) reduces to
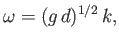 |
(11.36) |
because
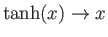 as
as
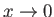 . It follows that the phase velocities and group velocities of gravity waves in shallow
water
all take the fixed value
. It follows that the phase velocities and group velocities of gravity waves in shallow
water
all take the fixed value
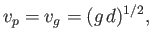 |
(11.37) |
irrespective of wave number.
We conclude that--unlike deep water waves--shallow water gravity waves are non-dispersive in nature (Fitzpatrick 2013). In other words, in shallow water,
waves pulses and plane waves all propagate at the same speed. It can be seen that the velocity (11.37) increases with increasing water depth.
For a plane wave of wave number
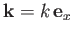 , in the limit
, in the limit 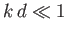 ,
Equation (11.19) yields
,
Equation (11.19) yields
![$\displaystyle \phi(x,z,t) = A\,[1+k^{\,2}\,(z+d)^2/2]\,\cos(\omega\,t-k\,x).$](img3956.png) |
(11.38) |
Hence, Equations (11.7) and (11.27) give [cf., Equations (11.45)-(11.48)]
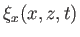 |
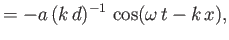 |
(11.39) |
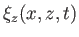 |
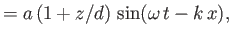 |
(11.40) |
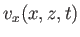 |
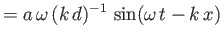 |
(11.41) |
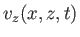 |
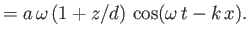 |
(11.42) |
Here, 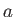 is again the amplitude of the vertical oscillation at the water's surface.
According to
the previous expressions, the passage of a shallow water gravity wave causes a water particle located a depth
is again the amplitude of the vertical oscillation at the water's surface.
According to
the previous expressions, the passage of a shallow water gravity wave causes a water particle located a depth 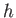 below the surface to execute an
elliptical orbit, of horizontal radius
below the surface to execute an
elliptical orbit, of horizontal radius 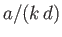 , and vertical radius
, and vertical radius
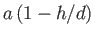 , about its equilibrium position. The orbit is
greatly elongated in the horizontal direction. Furthermore, its vertical radius decreases linearly with increasing depth such that
it becomes zero at the bottom (i.e., at
, about its equilibrium position. The orbit is
greatly elongated in the horizontal direction. Furthermore, its vertical radius decreases linearly with increasing depth such that
it becomes zero at the bottom (i.e., at 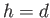 ). As before, whenever the particle's vertical displacement attains a maximum value the particle is
moving horizontally in the same direction as the wave, and vice versa.
). As before, whenever the particle's vertical displacement attains a maximum value the particle is
moving horizontally in the same direction as the wave, and vice versa.



Next: Energy of Gravity Waves
Up: Waves in Incompressible Fluids
Previous: Gravity Waves in Deep
Richard Fitzpatrick
2016-03-31
![]() , in the limit
, in the limit ![]() ,
Equation (11.19) yields
,
Equation (11.19) yields