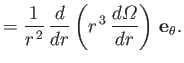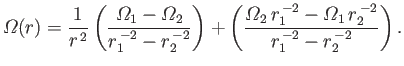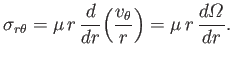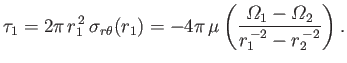Next: Flow in Slowly-Varying Channels
Up: Incompressible Viscous Flow
Previous: Poiseuille Flow
Consider two thin cylindrical shells with the same vertical axis. Let the inner and outer shells be of radius 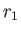 and
and  , respectively. Suppose
that the annular region
, respectively. Suppose
that the annular region
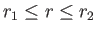 is filled with fluid of density
is filled with fluid of density  and viscosity
and viscosity 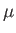 . Let the inner and outer cylinders rotate
at the constant angular velocities
. Let the inner and outer cylinders rotate
at the constant angular velocities
 and
and
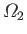 , respectively. We wish to determine the steady flow pattern set up within the fluid. Incidentally, this type of flow is generally known as Taylor-Couette flow,
after Maurice Couette and Geoffrey Taylor (1886-1975).
, respectively. We wish to determine the steady flow pattern set up within the fluid. Incidentally, this type of flow is generally known as Taylor-Couette flow,
after Maurice Couette and Geoffrey Taylor (1886-1975).
It is convenient to adopt cylindrical coordinates,  ,
,  ,
,  , whose symmetry axis coincides with the common axis of the two shells. Thus,
the inner and outer shells correspond to
, whose symmetry axis coincides with the common axis of the two shells. Thus,
the inner and outer shells correspond to 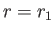 and
and 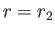 , respectively. Suppose that the flow velocity within the fluid
is written
, respectively. Suppose that the flow velocity within the fluid
is written
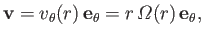 |
(10.30) |
where
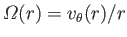 is the angular velocity profile. Application of the no slip condition at the two shells leads to the boundary
conditions
is the angular velocity profile. Application of the no slip condition at the two shells leads to the boundary
conditions
It follows from Section 1.19 that
 and
and
Hence, Equation (10.2) yields
 |
(10.35) |
and
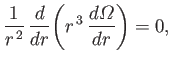 |
(10.36) |
assuming that 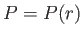 .
The solution of Equation (10.36) that satisfies the boundary conditions is
.
The solution of Equation (10.36) that satisfies the boundary conditions is
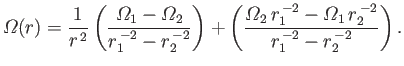 |
(10.37) |
It can be seen that this angular velocity profile is a combination of the solid body rotation profile
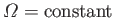 , and the
irrotational rotation profile
, and the
irrotational rotation profile
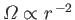 .
.
From Section 1.19, the only non-zero component of the viscous stress tensor within the fluid is
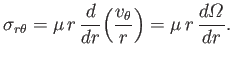 |
(10.38) |
Thus, the viscous torque (acting in the  -direction) per unit height (in the
-direction) per unit height (in the  -direction) exerted on the inner cylinder is
-direction) exerted on the inner cylinder is
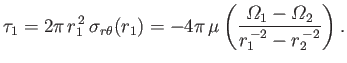 |
(10.39) |
Likewise, the torque per unit height exerted on the outer cylinder is
 |
(10.40) |
As expected, these two torques are equal and opposite, and act to make the two cylinders rotate at the same angular velocity (in which case,
the fluid between them rotates as a solid body).



Next: Flow in Slowly-Varying Channels
Up: Incompressible Viscous Flow
Previous: Poiseuille Flow
Richard Fitzpatrick
2016-03-31
![]() ,
, ![]() ,
, ![]() , whose symmetry axis coincides with the common axis of the two shells. Thus,
the inner and outer shells correspond to
, whose symmetry axis coincides with the common axis of the two shells. Thus,
the inner and outer shells correspond to ![]() and
and ![]() , respectively. Suppose that the flow velocity within the fluid
is written
, respectively. Suppose that the flow velocity within the fluid
is written