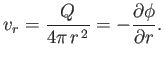Next: Dipole Point Sources
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Uniform Flow
Consider a point source, coincident with the origin, that emits fluid isotropically at the steady rate of  volumes per
unit time. By symmetry, we expect the associated steady flow pattern to be isotropic, and everywhere directed
radially away from the source. In other words,
volumes per
unit time. By symmetry, we expect the associated steady flow pattern to be isotropic, and everywhere directed
radially away from the source. In other words,
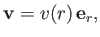 |
(7.29) |
where  is a spherical coordinate. Consider a spherical surface
is a spherical coordinate. Consider a spherical surface  of radius
of radius  whose center coincides with the source.
In a steady state, the rate at which fluid crosses this surface must be equal to the rate at which the source emits fluid.
Hence,
whose center coincides with the source.
In a steady state, the rate at which fluid crosses this surface must be equal to the rate at which the source emits fluid.
Hence,
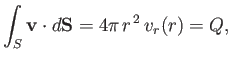 |
(7.30) |
which implies that
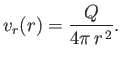 |
(7.31) |
Of course,
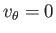 .
.
According to Equations (7.4), the Stokes stream function associated with a point source at the origin is such that
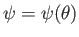 , and is obtained by integrating
, and is obtained by integrating
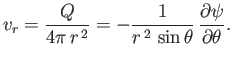 |
(7.32) |
It follows that
 |
(7.33) |
It is clear, from a comparison of Equations (7.10) and (7.33), that the previously
specified flow pattern is
irrotational. Hence, this pattern can also be derived from a velocity potential. In fact, by symmetry,
we expect that
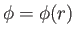 . The potential itself is obtained by integrating
. The potential itself is obtained by integrating
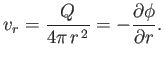 |
(7.34) |
It follows that
 |
(7.35) |



Next: Dipole Point Sources
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Uniform Flow
Richard Fitzpatrick
2016-03-31
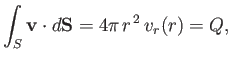
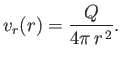
![]() , and is obtained by integrating
, and is obtained by integrating
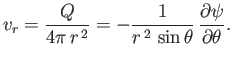
![]() . The potential itself is obtained by integrating
. The potential itself is obtained by integrating