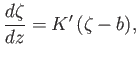Next: Free Streamline Theory
Up: Two-Dimensional Potential Flow
Previous: Conformal Maps
Schwarz-Christoffel Theorem
The Schwarz-Christoffel theorem is an important mathematical result that allows a polygonal boundary in the  -plane to be mapped conformally onto the real axis,
-plane to be mapped conformally onto the real axis,  , in the
, in the  -plane. It is conventional to map the region inside the polygon
in the
-plane. It is conventional to map the region inside the polygon
in the  -plane onto the upper half,
-plane onto the upper half,  , of the
, of the  -plane. If the interior angles of the polygon
are
-plane. If the interior angles of the polygon
are 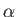 ,
, 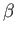 ,
, 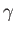 ,
, 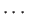 then the appropriate map is
then the appropriate map is
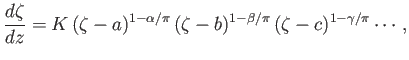 |
(6.79) |
where 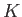 is a constant, and
is a constant, and 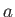 ,
,  ,
, 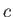 ,
,  are the (real) values of
are the (real) values of 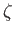 that correspond to the
vertices of the polygon (Milne-Thompson 2011).
that correspond to the
vertices of the polygon (Milne-Thompson 2011).
It is often convenient to take the point in the 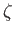 -plane that corresponds to one of the vertices of the polygon--say, that given by
-plane that corresponds to one of the vertices of the polygon--say, that given by 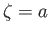 --to be
at infinity. In this case, the factor
--to be
at infinity. In this case, the factor  in Equation (6.79) becomes effectively constant, and can be absorbed into a new
constant of proportionality,
in Equation (6.79) becomes effectively constant, and can be absorbed into a new
constant of proportionality, 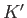 .
.
Figure:
Conformal transformation of a semi-infinite strip in the  -plane into the upper half of the
-plane into the upper half of the 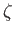 -plane.
-plane.
 |
Consider, for example, a semi-infinite strip in the  -plane, for which
-plane, for which  ,
,
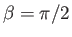 , and
, and
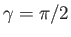 .
This is mapped onto the upper half of the
.
This is mapped onto the upper half of the 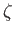 -plane, with the zero-angle vertex corresponding to a point at
infinity in the
-plane, with the zero-angle vertex corresponding to a point at
infinity in the 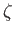 -plane, by means of the transformation
-plane, by means of the transformation
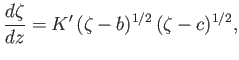 |
(6.80) |
where 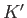 is real and positive.
We can integrate the previous expression to give
is real and positive.
We can integrate the previous expression to give
![$\displaystyle \zeta = \frac{1}{2}\,(b+c)+\frac{1}{2}\,(b-c)\,\cosh[K'\,(z-z_0)].$](img2154.png) |
(6.81) |
Here, the points 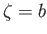 and
and 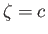 in the
in the 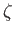 -plane correspond to the vertices
-plane correspond to the vertices 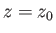 and
and
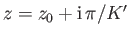 , respectively,
in the
, respectively,
in the  -plane. (See Figure 6.12.)
-plane. (See Figure 6.12.)
Suppose that 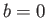 ,
, 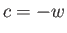 ,
,  , and
, and 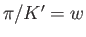 . In this case, the transformation (6.81) becomes
. In this case, the transformation (6.81) becomes
![$\displaystyle \zeta = \frac{w}{2}\left[\cosh\left(\pi\,\frac{z}{w}\right)-1\right],$](img2161.png) |
(6.82) |
which implies that
The transformation (6.82) maps the semi-infinite strip in the  -plane that is bounded by the lines
-plane that is bounded by the lines 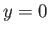 ,
,  , and
, and 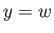 into the upper half of the
into the upper half of the
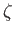 -plane. The transformation also maps the origin of the
-plane. The transformation also maps the origin of the 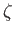 -plane to the origin of the
-plane to the origin of the  -plane, and
the
-plane, and
the 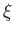 -axis to the lines
-axis to the lines 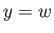 ,
,  , and
, and 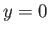 . Now, in the
. Now, in the 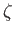 -plane,
-plane,
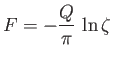 |
(6.85) |
is the complex potential associated with a line source of strength 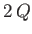 , located at the origin. By symmetry, the
, located at the origin. By symmetry, the
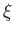 -axis corresponds to a streamline, and can, therefore, be replaced by a rigid boundary. It follows that, in the
-axis corresponds to a streamline, and can, therefore, be replaced by a rigid boundary. It follows that, in the
 -plane, the same potential is that due to a line source, of strength
-plane, the same potential is that due to a line source, of strength 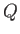 , located in the lower left-hand corner of a semi-infinite strip
bounded by rigid planes at
, located in the lower left-hand corner of a semi-infinite strip
bounded by rigid planes at 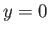 ,
,  , and
, and 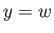 . (Incidentally, the source strength in the
. (Incidentally, the source strength in the  -plane is
-plane is
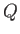 , rather than
, rather than 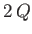 , because, by symmetry, half the output from the source in the
, because, by symmetry, half the output from the source in the 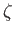 -plane goes below the
-plane goes below the 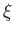 -axis and, therefore, does not map to the semi-infinite strip in the
-axis and, therefore, does not map to the semi-infinite strip in the  -plane.) The corresponding stream function is
-plane.) The corresponding stream function is
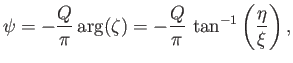 |
(6.86) |
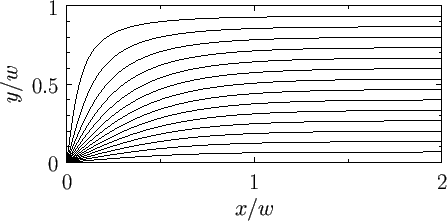
and is illustrated in Figure 6.13.
Figure:
Stream function due to a line source located in the left-hand corner of a semi-infinite strip
bounded by rigid planes at 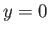 ,
,  , and
, and 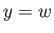 .
.
 |
An infinite strip in the  -plane is a polygon with two zero-angle vertices, both at infinity. The required transformation
follows from Equation (6.79) by setting
-plane is a polygon with two zero-angle vertices, both at infinity. The required transformation
follows from Equation (6.79) by setting
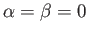 ,
,
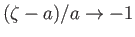 , and
, and
 .
Thus, we obtain
.
Thus, we obtain
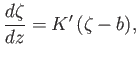 |
(6.87) |
which can be integrated to give
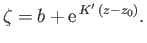 |
(6.88) |
This transformation maps the point 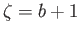 to the point
to the point 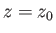 , the
, the 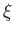 -axis to the two lines
-axis to the two lines
 and
and
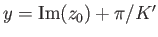 ,
and the upper half of the
,
and the upper half of the 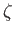 -plane to the region between the lines
-plane to the region between the lines
 and
and
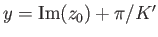 , as illustrated in
Figure 6.14. It is clear that the transformation (6.60), studied in the preceding section, is just a special
case of the transformation (6.88).
, as illustrated in
Figure 6.14. It is clear that the transformation (6.60), studied in the preceding section, is just a special
case of the transformation (6.88).
Figure:
Conformal transformation of an infinite strip in the  -plane into the upper half of the
-plane into the upper half of the 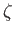 -plane.
-plane.
 |



Next: Free Streamline Theory
Up: Two-Dimensional Potential Flow
Previous: Conformal Maps
Richard Fitzpatrick
2016-01-22
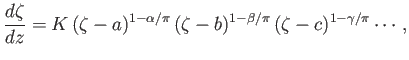
![]() -plane that corresponds to one of the vertices of the polygon--say, that given by
-plane that corresponds to one of the vertices of the polygon--say, that given by ![]() --to be
at infinity. In this case, the factor
--to be
at infinity. In this case, the factor ![]() in Equation (6.79) becomes effectively constant, and can be absorbed into a new
constant of proportionality,
in Equation (6.79) becomes effectively constant, and can be absorbed into a new
constant of proportionality, ![]() .
.

![]() -plane, for which
-plane, for which ![]() ,
,
![]() , and
, and
![]() .
This is mapped onto the upper half of the
.
This is mapped onto the upper half of the ![]() -plane, with the zero-angle vertex corresponding to a point at
infinity in the
-plane, with the zero-angle vertex corresponding to a point at
infinity in the ![]() -plane, by means of the transformation
-plane, by means of the transformation
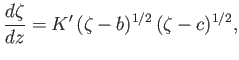
![]() ,
, ![]() ,
, ![]() , and
, and ![]() . In this case, the transformation (6.81) becomes
. In this case, the transformation (6.81) becomes
![$\displaystyle =\frac{w}{2}\left[\cosh\left(\pi\,\frac{x}{w}\right)\cos\left(\pi\,\frac{y}{w}\right)-1\right],$](img2163.png)
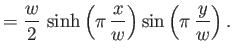
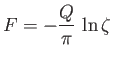
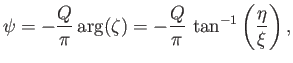

![]() -plane is a polygon with two zero-angle vertices, both at infinity. The required transformation
follows from Equation (6.79) by setting
-plane is a polygon with two zero-angle vertices, both at infinity. The required transformation
follows from Equation (6.79) by setting
![]() ,
,
![]() , and
, and
![]() .
Thus, we obtain
.
Thus, we obtain