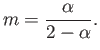Inviscid Flow Past a Semi-Infinite Wedge

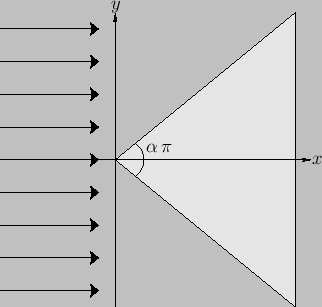
Consider the situation, illustrated in Figure 5.10, in which incompressible irrotational flow is incident on a impenetrable rigid wedge whose apex subtends an angle $\alpha\,\pi$ . Let the cross-section of the wedge in the $x$ -$y$ plane be both $z$ -independent and symmetric about the $x$ -axis. Furthermore, let the apex of the wedge lie at $x=y=0$ . Finally, let the upstream flow a large distance from the wedge be parallel to the $x$ -axis.

Figure 5.10: Inviscid flow past a wedge.

Because the flow is two-dimensional, incompressible, and irrotational, it can be represented in terms of a stream function that satisfies Laplace's equation. Moreover, in cylindrical coordinates, this equation takes the form (5.61). The boundary conditions on the stream function are

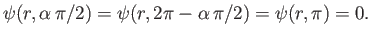$$\psi(r,\alpha\,\pi/2) =\psi(r,2\pi-\alpha\,\pi/2)=\psi(r,\pi)=0.$$ (5.126)

The first two boundary conditions ensure that the normal velocity at the surface of the wedge is zero. The third boundary condition follows from the observation that, by symmetry, the streamline that meets the apex of the wedge splits in two, and then flows along its top and bottom boundaries, combined with the well-known result that $\psi$ is constant on a streamline. It is easily demonstrated that

$$\psi(r,\theta) = \frac{A}{1+m}\,r^{\,1+m}\,\sin\left[(1+m)\,(\pi-\theta)\right]$$ (5.127)

is a solution of Equation (5.61). Moreover, this solution satisfies the boundary conditions provided 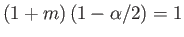$(1+m)\,(1-\alpha/2) = 1$ , or

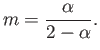$$m=\frac{\alpha}{2-\alpha}.$$ (5.128)

Because, as is well known, the solutions to Laplace's equation (for problems with well-posed boundary conditions) are unique (Riley 1974), we can be sure that Equation (5.127) is the correct solution to the problem under investigation. According to this solution, the tangential velocity on the surface of the wedge is given by

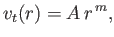$$v_t(r) = A\,r^{\,m},$$ (5.129)

where $m\geq 0$ . Note that the tangential velocity is zero at the apex of the wedge. Because the normal velocity is also zero at this point, we conclude that the apex is a stagnation point of the flow. Figure 5.11 shows the streamlines of the flow for the case $\alpha=1/2$ .

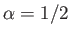Figure: Streamlines of inviscid incompressible irrotational flow past a 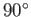$90^\circ$ wedge.