


Next: Coordinate Transformations
Up: Vectors and Vector Fields
Previous: Vector Algebra
Consider a Cartesian coordinate system  , consisting of
an origin,
, consisting of
an origin, 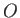 , and three mutually perpendicular coordinate axes,
, and three mutually perpendicular coordinate axes, 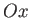 ,
, 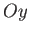 , and
, and
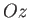 . (See Figure A.4.) Such a system is said to be right-handed if, when looking along the
. (See Figure A.4.) Such a system is said to be right-handed if, when looking along the 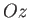 direction, a
direction, a 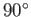 clockwise
rotation about
clockwise
rotation about 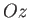 is required to take
is required to take 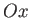 into
into  . Otherwise, it is said to be left-handed. It is conventional to always use a right-handed coordinate system.
. Otherwise, it is said to be left-handed. It is conventional to always use a right-handed coordinate system.
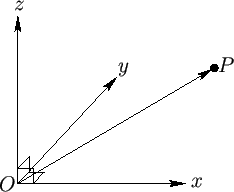
Figure A.4:
A right-handed Cartesian coordinate system.
 |
It is convenient to define unit vectors, 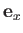 ,
,  , and
, and 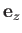 , parallel to
, parallel to 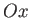 ,
, 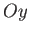 , and
, and 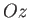 , respectively.
Incidentally, a unit vector is a vector whose magnitude is unity. The position vector,
, respectively.
Incidentally, a unit vector is a vector whose magnitude is unity. The position vector,  , of some general point
, of some general point 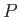 whose Cartesian coordinates
are (
whose Cartesian coordinates
are ( ,
,  ,
,  ) is then given by
) is then given by
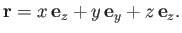 |
(A.11) |
In other words, we can get from 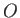 to
to 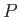 by moving a distance
by moving a distance  parallel to
parallel to 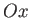 , then a distance
, then a distance
 parallel to
parallel to 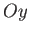 , and then a distance
, and then a distance  parallel to
parallel to 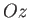 . Similarly, if
. Similarly, if 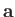 is an arbitrary vector then
is an arbitrary vector then
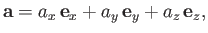 |
(A.12) |
where 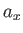 ,
, 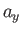 , and
, and 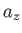 are termed the Cartesian components of
are termed the Cartesian components of 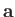 . It is conventional to write
. It is conventional to write
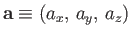 .
It follows that
.
It follows that
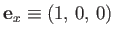 ,
,
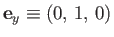 , and
, and
 . Of course,
. Of course,
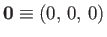 .
.
According to the three-dimensional generalization of the Pythagorean theorem, the distance
 is
given by
is
given by
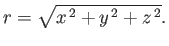 |
(A.13) |
By analogy, the magnitude of a general vector 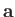 takes the form
takes the form
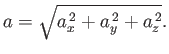 |
(A.14) |
If
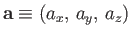 and
and
 then it is
easily demonstrated that
then it is
easily demonstrated that
 |
(A.15) |
Furthermore, if 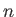 is a scalar then it is apparent that
is a scalar then it is apparent that
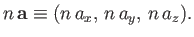 |
(A.16) |



Next: Coordinate Transformations
Up: Vectors and Vector Fields
Previous: Vector Algebra
Richard Fitzpatrick
2016-01-22

![]() ,
, ![]() , and
, and ![]() , parallel to
, parallel to ![]() ,
, ![]() , and
, and ![]() , respectively.
Incidentally, a unit vector is a vector whose magnitude is unity. The position vector,
, respectively.
Incidentally, a unit vector is a vector whose magnitude is unity. The position vector, ![]() , of some general point
, of some general point ![]() whose Cartesian coordinates
are (
whose Cartesian coordinates
are (![]() ,
, ![]() ,
, ![]() ) is then given by
) is then given by
![]() is
given by
is
given by
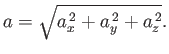
![]() and
and
![]() then it is
easily demonstrated that
then it is
easily demonstrated that