


Next: Homenergic Homentropic Flow
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Thin-Airfoil Theory
Crocco's Theorem
Bernoulli's theorem for the steady, inviscid flow of an ideal gas, in the absence of body forces, implies that,
on a given streamline,
 |
(15.85) |
where 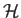 is the specific enthalpy,
is the specific enthalpy,
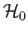 the stagnation enthalpy, and
the stagnation enthalpy, and  the flow velocity. (See Section 14.5.)
The fluid equation of motion, (14.31), reduces to
the flow velocity. (See Section 14.5.)
The fluid equation of motion, (14.31), reduces to
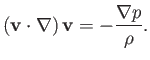 |
(15.86) |
However, according to Equation (A.171),
where
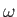
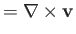 . Hence, we obtain
. Hence, we obtain
Now, Equation (14.29) implies that
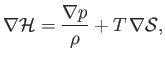 |
(15.89) |
where  is the temperature, and
is the temperature, and 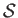 the specific entropy. Moreover, Equation (15.85)
yields
the specific entropy. Moreover, Equation (15.85)
yields
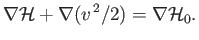 |
(15.90) |
Thus, we arrive at Crocco's theorem:
In most aerodynamic flows, the fluid originates from a common reservoir, which implies that the stagnation enthalpy,
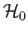 , is
the same on all streamlines. Such flow is termed homenergic. It follows from Equation (14.18) that the stagnation temperature,
, is
the same on all streamlines. Such flow is termed homenergic. It follows from Equation (14.18) that the stagnation temperature, 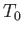 , is
the same on all streamlines in homenergic flow.
According to Crocco's theorem, an irrotational
(i.e.,
, is
the same on all streamlines in homenergic flow.
According to Crocco's theorem, an irrotational
(i.e.,
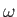
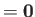 everywhere) homenergic (i.e.,
everywhere) homenergic (i.e.,
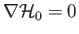 everywhere) flow pattern is also homentropic (i.e.,
everywhere) flow pattern is also homentropic (i.e.,
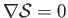 everywhere). Conversely, a homenergic, homentropic flow pattern is also irrotational (at least, in two dimensions, where
everywhere). Conversely, a homenergic, homentropic flow pattern is also irrotational (at least, in two dimensions, where  and
and
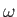 cannot be parallel to one another).
cannot be parallel to one another).



Next: Homenergic Homentropic Flow
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Thin-Airfoil Theory
Richard Fitzpatrick
2016-01-22

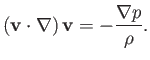
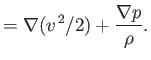
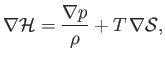
![]() , is
the same on all streamlines. Such flow is termed homenergic. It follows from Equation (14.18) that the stagnation temperature,
, is
the same on all streamlines. Such flow is termed homenergic. It follows from Equation (14.18) that the stagnation temperature, ![]() , is
the same on all streamlines in homenergic flow.
According to Crocco's theorem, an irrotational
(i.e.,
, is
the same on all streamlines in homenergic flow.
According to Crocco's theorem, an irrotational
(i.e.,
![]()
![]() everywhere) homenergic (i.e.,
everywhere) homenergic (i.e.,
![]() everywhere) flow pattern is also homentropic (i.e.,
everywhere) flow pattern is also homentropic (i.e.,
![]() everywhere). Conversely, a homenergic, homentropic flow pattern is also irrotational (at least, in two dimensions, where
everywhere). Conversely, a homenergic, homentropic flow pattern is also irrotational (at least, in two dimensions, where ![]() and
and
![]() cannot be parallel to one another).
cannot be parallel to one another).