


Next: Planetary Rotation
Up: Terrestrial Ocean Tides
Previous: Expansion of Tide Generating
A surface harmonic of degree 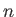 (where
(where 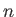 is a non-negative integer), denoted
is a non-negative integer), denoted
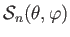 , is defined as a well-behaved solution
to
, is defined as a well-behaved solution
to
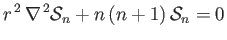 |
(12.36) |
on the surface of a sphere (i.e.,  constant). Here,
constant). Here, 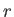 ,
, 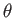 ,
, 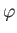 are standard spherical coordinates, and
are standard spherical coordinates, and
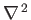 is the Laplacian operator. It follows that (Love 1927)
is the Laplacian operator. It follows that (Love 1927)
![$\displaystyle {\cal S}_n(\theta,\varphi) = \sum_{m=0,n} \left[c_n^{\,m}\,P_n^{\...
...\,\cos(m\,\varphi) + d_n^{\,m}\,P_n^{\,m}(\cos\theta)\,\sin(m\,\varphi)\right],$](img4313.png) |
(12.37) |
where the 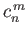 and
and 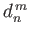 are arbitrary coefficients, and the
are arbitrary coefficients, and the
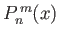 associated Legendre functions.
associated Legendre functions.
A solid harmonic of degree 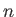 (where
(where 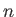 is a non-negative integer), denoted
is a non-negative integer), denoted
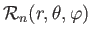 , is defined as a well-behaved solution
to
, is defined as a well-behaved solution
to
 |
(12.38) |
in the interior of a sphere (i.e., the region 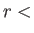 constant). It follows that (Love 1927)
constant). It follows that (Love 1927)
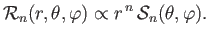 |
(12.39) |
In particular, the functions
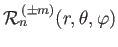 and
and
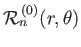 , introduced in Section 12.3,
are solid harmonics of degree
, introduced in Section 12.3,
are solid harmonics of degree 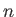 . Note that the Cartesian coordinates
. Note that the Cartesian coordinates 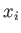 (where
(where 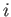 runs from
runs from  to
to 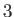 ) are solid
harmonics of degree
) are solid
harmonics of degree  . Moreover,
. Moreover,
 is a solid harmonic of degree
is a solid harmonic of degree 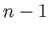 . Finally,
. Finally,
 ,
specified in Equation (12.35), is a solid harmonic of degree 2.
,
specified in Equation (12.35), is a solid harmonic of degree 2.
The following results regarding solid harmonics are useful (Love 1927):
Here, use has been made of the Einstein summation convention (Riley 1974).



Next: Planetary Rotation
Up: Terrestrial Ocean Tides
Previous: Expansion of Tide Generating
Richard Fitzpatrick
2016-01-22
![]() (where
(where ![]() is a non-negative integer), denoted
is a non-negative integer), denoted
![]() , is defined as a well-behaved solution
to
, is defined as a well-behaved solution
to