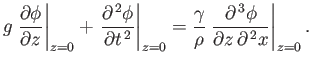Next: Capillary Waves
Up: Waves in Incompressible Fluids
Previous: Steady Flow over a
Surface Tension
As described in Chapter 3, there is a positive excess energy per unit area, 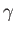 , associated with an interface between two immiscible fluids. The quantity
, associated with an interface between two immiscible fluids. The quantity 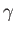 can also be interpreted as a surface tension. Let us now incorporate surface tension into
our analysis. Suppose that the interface lies at
can also be interpreted as a surface tension. Let us now incorporate surface tension into
our analysis. Suppose that the interface lies at
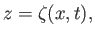 |
(11.112) |
where 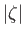 is small. Thus, the unperturbed interface corresponds to the plane
is small. Thus, the unperturbed interface corresponds to the plane  . The unit normal to the interface is
. The unit normal to the interface is
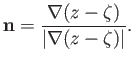 |
(11.113) |
It follows that
The Young-Laplace Equation (see Section 3.2) yields
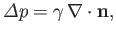 |
(11.116) |
where
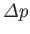 is the jump in pressure seen crossing the interface in the opposite direction to
is the jump in pressure seen crossing the interface in the opposite direction to 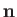 .
However, from Equations (11.114) and (11.115), we have
.
However, from Equations (11.114) and (11.115), we have
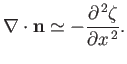 |
(11.117) |
Hence, Equation (11.116) gives
![$\displaystyle [p]_{z=0_-}^{z=0_+} = \gamma\,\frac{\partial^{\,2}\zeta}{\partial x^{\,2}}.$](img4138.png) |
(11.118) |
This expression is the generalization of Equation (11.99) that takes surface tension into account.
Suppose that the interface in question is that between a body of water, of density  and depth
and depth 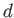 , and the atmosphere. Let the unperturbed water lie
between
, and the atmosphere. Let the unperturbed water lie
between 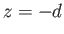 and
and  , and let the unperturbed atmosphere occupy the region
, and let the unperturbed atmosphere occupy the region  . In the limit in which the density
of the atmosphere is neglected, the pressure in the atmosphere takes the fixed value
. In the limit in which the density
of the atmosphere is neglected, the pressure in the atmosphere takes the fixed value 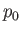 , whereas the pressure
just below the surface of the water is
, whereas the pressure
just below the surface of the water is
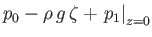 . Here,
. Here, 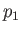 is the pressure perturbation
due to the wave. The relation (11.118) yields
is the pressure perturbation
due to the wave. The relation (11.118) yields
 |
(11.119) |
where 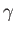 is the surface tension at an air/water interface. However,
is the surface tension at an air/water interface. However,
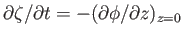 ,
where
,
where 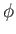 is the perturbed velocity potential of the water. Moreover, from Equation (11.9),
is the perturbed velocity potential of the water. Moreover, from Equation (11.9),
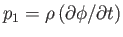 .
Hence, the previous expression gives
.
Hence, the previous expression gives
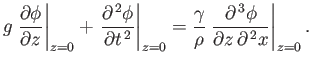 |
(11.120) |
This relation, which is a generalization of Equation (11.15), is the condition satisfied at a free surface in the presence of
non-negligible surface tension. Applying this boundary condition to the general solution, (11.19) (which already satisfies the boundary
condition at the bottom), we obtain the dispersion relation
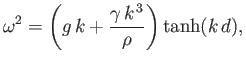 |
(11.121) |
which is a generalization of Equation (11.21) that takes surface tension into account.



Next: Capillary Waves
Up: Waves in Incompressible Fluids
Previous: Steady Flow over a
Richard Fitzpatrick
2016-01-22
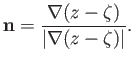
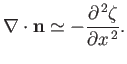
![]() and depth
and depth ![]() , and the atmosphere. Let the unperturbed water lie
between
, and the atmosphere. Let the unperturbed water lie
between ![]() and
and ![]() , and let the unperturbed atmosphere occupy the region
, and let the unperturbed atmosphere occupy the region ![]() . In the limit in which the density
of the atmosphere is neglected, the pressure in the atmosphere takes the fixed value
. In the limit in which the density
of the atmosphere is neglected, the pressure in the atmosphere takes the fixed value ![]() , whereas the pressure
just below the surface of the water is
, whereas the pressure
just below the surface of the water is
![]() . Here,
. Here, ![]() is the pressure perturbation
due to the wave. The relation (11.118) yields
is the pressure perturbation
due to the wave. The relation (11.118) yields