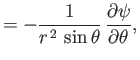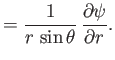Axisymmetric Stokes Flow

Let 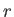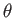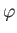$r$ , $\theta$ , $\varphi$ be standard spherical coordinates. Consider axisymmetric Stokes flow such that

$${\bf v}({\bf r}) = v_r(r,\theta)\,{\bf e}_r + v_\theta(r,\theta)\,{\bf e}_\theta.$$ (10.83)

According to Equations (A.175) and (A.176), we can automatically satisfy the incompressibility constraint (10.79) by writing (see Section 7.4)

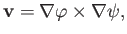$${\bf v} =\nabla\varphi\times\nabla\psi,$$ (10.84)

where 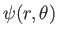$\psi(r,\theta)$ is the Stokes stream function (i.e., 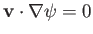${\bf v}\cdot\nabla\psi = 0$ ). It follows that

$$v_r(r,\theta) = - \frac{1}{r^{\,2}\,\sin\theta}\,\frac{\partial\psi}{\partial \theta},$$ (10.85)

$$v_\theta(r,\theta) = \frac{1}{r\,\sin\theta}\,\frac{\partial\psi}{\partial r}.$$ (10.86)

Moreover, according to Section C.4, 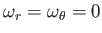$\omega_r=\omega_\theta=0$ , and

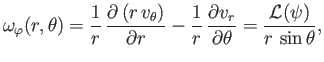$$\omega_\varphi(r,\theta) = \frac{1}{r}\,\frac{\partial\,(r\,v_\th... ...r}\,\frac{\partial v_r}{\partial\theta} = \frac{{\cal L}(\psi)}{r\,\sin\theta},$$ (10.87)

where (see Section 7.4)

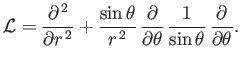$${\cal L} = \frac{\partial^{\,2}}{\partial r^{\,2}} + \frac{\sin\t... ...artial}{\partial\theta}\,\frac{1}{\sin\theta}\,\frac{\partial}{\partial\theta}.$$ (10.88)

Hence, given that 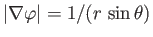$\vert\nabla\varphi\vert=1/(r\,\sin\theta)$ , we can write

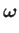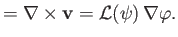$$\mbox{\boldmath$\omega$} =\nabla\times{\bf v} = {\cal L}(\psi)\,\nabla\varphi.$$ (10.89)

It follows from Equations (A.176) and (A.178) that

$$\nabla\times \mbox{\boldmath$\omega$} = \nabla\varphi\times \nabla[-{\cal L}(\psi)].$$ (10.90)

Thus, by analogy with Equations (10.84) and (10.89), and making use of Equations (A.173) and (A.177), we obtain

$$\nabla\times (\nabla\times \mbox{\boldmath$\omega$} ) = -\nabla^{\,2} \mbox{\boldmath$\omega$} = - {\cal L}^{\,2}(\psi)\,\nabla\varphi.$$ (10.91)

Equation (10.82) implies that

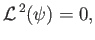$${\cal L}^{\,2}(\psi) = 0,$$ (10.92)

which is the governing equation for axisymmetric Stokes flow. In addition, Equations (10.81) and (10.90) yield

$$\nabla P = \mu\,\nabla\varphi\times \nabla[{\cal L}(\psi)].$$ (10.93)