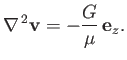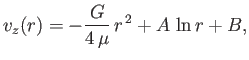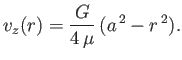Next: Taylor-Couette Flow
Up: Incompressible Viscous Flow
Previous: Flow Down an Inclined
Poiseuille Flow
Steady viscous fluid flow driven by an effective pressure gradient established between the two ends of a long straight pipe of uniform
circular cross-section is generally known as Poiseuille flow, because it was first studied experimentally by
Jean Poiseuille (1797-1869) in 1838. Suppose that the pipe is of radius 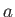 . Let us adopt cylindrical coordinates whose symmetry axis coincides with that of the
pipe. Thus,
. Let us adopt cylindrical coordinates whose symmetry axis coincides with that of the
pipe. Thus,  measures distance along the pipe,
measures distance along the pipe,  corresponds to the center of the pipe, and
corresponds to the center of the pipe, and  corresponds to the pipe wall.
Suppose that
corresponds to the pipe wall.
Suppose that
 |
(10.23) |
is the uniform effective pressure gradient along the pipe, and
 |
(10.24) |
the time independent velocity profile driven by this gradient. It follows from Section 1.19 that
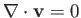 and
and
 .
Hence, Equation (10.2) reduces to
.
Hence, Equation (10.2) reduces to
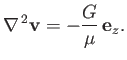 |
(10.25) |
Taking the  -component of this equation, we obtain
-component of this equation, we obtain
 |
(10.26) |
where use has been made of Equation (1.155). The most general solution of the
previous equation is
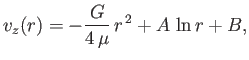 |
(10.27) |
where 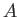 and
and 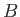 are arbitrary constants. The physical constraints are that the flow velocity is
non-singular at the center of the pipe (which implies that
are arbitrary constants. The physical constraints are that the flow velocity is
non-singular at the center of the pipe (which implies that  ), and is zero at the edge of the pipe [i.e.,
), and is zero at the edge of the pipe [i.e., 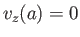 ], in
accordance with the no slip condition. Thus, we obtain
], in
accordance with the no slip condition. Thus, we obtain
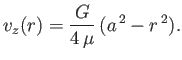 |
(10.28) |
The volume flux of fluid down the pipe is
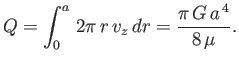 |
(10.29) |
According to the previous analysis, the quantity 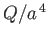 should be directly proportional to the effective
pressure gradient along the pipe. The accuracy with which experimental observations
show that this is indeed the case (at relatively low Reynolds number) is strong evidence in favor of the assumptions that there is no slip at the pipe
walls, and that the flow is non-turbulent. In fact, the result (10.29), which is known as Poiseuille's law, is valid experimentally provided the Reynolds number of the flow,
should be directly proportional to the effective
pressure gradient along the pipe. The accuracy with which experimental observations
show that this is indeed the case (at relatively low Reynolds number) is strong evidence in favor of the assumptions that there is no slip at the pipe
walls, and that the flow is non-turbulent. In fact, the result (10.29), which is known as Poiseuille's law, is valid experimentally provided the Reynolds number of the flow,
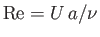 , remains less than about
, remains less than about
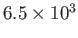 . Here,
. Here,
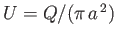 is the mean flow speed. On the other hand, if the
Reynolds number exceeds the critical value
is the mean flow speed. On the other hand, if the
Reynolds number exceeds the critical value
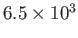 then the flow in the pipe becomes turbulent, and Poiseuille's law breaks down.
then the flow in the pipe becomes turbulent, and Poiseuille's law breaks down.



Next: Taylor-Couette Flow
Up: Incompressible Viscous Flow
Previous: Flow Down an Inclined
Richard Fitzpatrick
2016-01-22