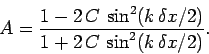Next: An improved 1-d diffusion
Up: The diffusion equation
Previous: von Neumann stability analysis
The Crank-Nicholson scheme
Let us revisit our temporal differencing scheme:
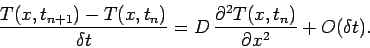 |
(210) |
Note that the right-hand side is evaluated entirely at the start
of the time-step: i.e., at 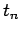 . This type of
temporal differencing scheme is termed an explicit scheme. Now, explicit schemes are
very straightforward to implement, but are also notoriously prone to numerical instabilities.
Fortunately, we can often overcome these instabilities by making our differencing
scheme implicit in nature. An implicit scheme is one in which the right-hand
side is evaluated partly (or wholly) at the end of the time-step: i.e., at
. This type of
temporal differencing scheme is termed an explicit scheme. Now, explicit schemes are
very straightforward to implement, but are also notoriously prone to numerical instabilities.
Fortunately, we can often overcome these instabilities by making our differencing
scheme implicit in nature. An implicit scheme is one in which the right-hand
side is evaluated partly (or wholly) at the end of the time-step: i.e., at 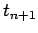 .
Unfortunately, implicit schemes are generally a great deal more complicated to implement
than explicit schemes.
.
Unfortunately, implicit schemes are generally a great deal more complicated to implement
than explicit schemes.
The well-known Crank-Nicholson implicit method for solving the diffusion equation involves
taking the
average of the right-hand side between the beginning and end of the time-step. In other words,
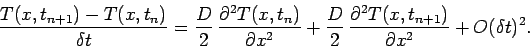 |
(211) |
As indicated by the error term, this method is actually second-order in time.
Adopting our usual spatial differencing scheme, the above expression yields
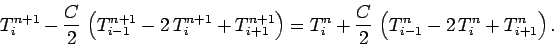 |
(212) |
When we perform a von Neumann stability analysis of the above scheme, we obtain the
following expression for the amplification factor:
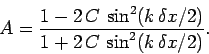 |
(213) |
Note that 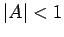 for all values of
for all values of 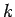 . It follows that the Crank-Nicholson
scheme is unconditionally stable. Unfortunately, Eq. (212) constitutes
a tridiagonal matrix equation linking the
. It follows that the Crank-Nicholson
scheme is unconditionally stable. Unfortunately, Eq. (212) constitutes
a tridiagonal matrix equation linking the 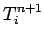 and the
and the 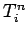 . Thus, the
price we pay for the high accuracy and unconditional stability of the Crank-Nicholson
scheme is having to invert a tridiagonal matrix equation at each time-step. Usually,
this price is well worth paying.
. Thus, the
price we pay for the high accuracy and unconditional stability of the Crank-Nicholson
scheme is having to invert a tridiagonal matrix equation at each time-step. Usually,
this price is well worth paying.



Next: An improved 1-d diffusion
Up: The diffusion equation
Previous: von Neumann stability analysis
Richard Fitzpatrick
2006-03-29