


Next: Basins of attraction
Up: The chaotic pendulum
Previous: The Poincaré section
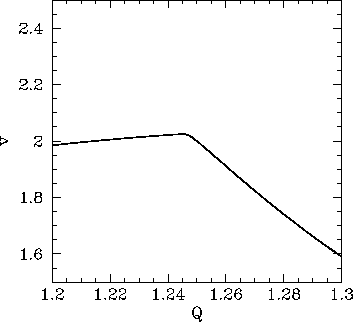
Figure 30:
The 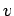 -coordinate of the Poincaré section of a time-asymptotic orbit
plotted against the quality-factor
-coordinate of the Poincaré section of a time-asymptotic orbit
plotted against the quality-factor 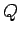 . Data
calculated numerically for
. Data
calculated numerically for
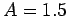 ,
, 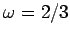 ,
, 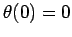 ,
, 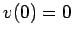 ,
,
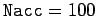 , and
, and 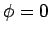 .
.
 |
Suppose that we now gradually increase the quality-factor 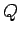 . What happens to the
simple orbit shown in Fig. 28? It turns out that, at first, nothing particularly exciting
happens. The size of the orbit gradually increases, indicating a corresponding increase in
the amplitude of the pendulum's motion, but the general nature of the motion remains unchanged.
However, something interesting does occur when
. What happens to the
simple orbit shown in Fig. 28? It turns out that, at first, nothing particularly exciting
happens. The size of the orbit gradually increases, indicating a corresponding increase in
the amplitude of the pendulum's motion, but the general nature of the motion remains unchanged.
However, something interesting does occur when 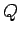 is increased beyond about
is increased beyond about  .
Figure 30 shows the
.
Figure 30 shows the 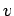 -coordinate of the orbit's Poincaré section plotted
against
-coordinate of the orbit's Poincaré section plotted
against 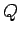 in the range
in the range 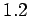 and
and 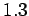 . Note the sharp downturn
in the curve at
. Note the sharp downturn
in the curve at 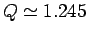 . What does this signify? Well, Fig. 31 shows
the time-asymptotic phase-space orbit just before the downturn (i.e.,
at
. What does this signify? Well, Fig. 31 shows
the time-asymptotic phase-space orbit just before the downturn (i.e.,
at 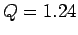 ), and Fig. 32 shows the orbit somewhat after the downturn
(i.e., at
), and Fig. 32 shows the orbit somewhat after the downturn
(i.e., at 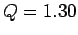 ). It is clear that the downturn is associated with a
sudden change in the nature of the pendulum's time-asymptotic phase-space orbit. Prior to the downturn, the orbit
spends as much time in the region
). It is clear that the downturn is associated with a
sudden change in the nature of the pendulum's time-asymptotic phase-space orbit. Prior to the downturn, the orbit
spends as much time in the region 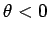 as in the region
as in the region 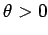 . However,
after the downturn the orbit spends the majority of its time in the region
. However,
after the downturn the orbit spends the majority of its time in the region 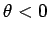 .
In other words, after the downturn the pendulum bob favours the region to the left of
the pendulum's vertical. This is somewhat surprising, since there is nothing in the
pendulum's equations of motion which differentiates between the regions to the left
and to the right of the vertical. We refer to a solution of this type--which fails
to realize the full symmetry of the dynamical system in question--as a symmetry
breaking solution. In this case, because the particular symmetry which is broken is
a spatial symmetry, we refer to the process by which the symmetry breaking solution
suddenly appears, as the control parameter
.
In other words, after the downturn the pendulum bob favours the region to the left of
the pendulum's vertical. This is somewhat surprising, since there is nothing in the
pendulum's equations of motion which differentiates between the regions to the left
and to the right of the vertical. We refer to a solution of this type--which fails
to realize the full symmetry of the dynamical system in question--as a symmetry
breaking solution. In this case, because the particular symmetry which is broken is
a spatial symmetry, we refer to the process by which the symmetry breaking solution
suddenly appears, as the control parameter 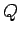 is adjusted, as spatial symmetry breaking.
Needless to say, spatial symmetry breaking is an intrinsically non-linear process--it
cannot take place in dynamical systems possessing linear equations of motion.
is adjusted, as spatial symmetry breaking.
Needless to say, spatial symmetry breaking is an intrinsically non-linear process--it
cannot take place in dynamical systems possessing linear equations of motion.
Figure 31:
Equally spaced (in time) points on a time-asymptotic orbit in phase-space.
Data calculated numerically for 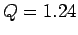 ,
, 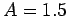 ,
, 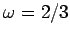 ,
, 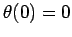 ,
,
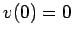 , and
, and
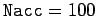 .
.
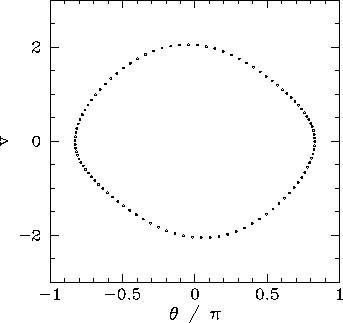 |
Figure 32:
Equally spaced (in time) points on a time-asymptotic orbit in phase-space.
Data calculated
numerically for 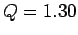 ,
, 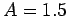 ,
, 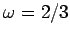 ,
, 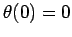 ,
,
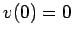 , and
, and
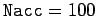 .
.
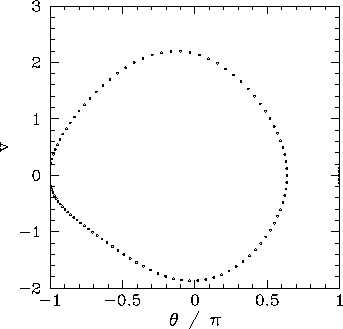 |
It stands to reason that since the pendulum's equations of motion favour neither the
left nor the right then the left-favouring orbit pictured in Fig. 32 must be accompanied
by a mirror image right-favouring orbit. How do we obtain this mirror image orbit?
It turns out that all we have to do is keep the physics parameters 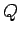 ,
, 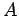 , and
, and 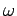 fixed, but change the initial conditions
fixed, but change the initial conditions 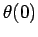 and
and 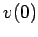 . Figure 33 shows
a time-asymptotic phase-space orbit calculated with the same physics parameters used in Fig. 32, but
with the initial conditions
. Figure 33 shows
a time-asymptotic phase-space orbit calculated with the same physics parameters used in Fig. 32, but
with the initial conditions 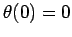 and
and 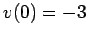 , instead of
, instead of 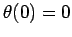 and
and
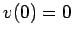 . It can be seen that the orbit is indeed the mirror image of that pictured in Fig. 32.
. It can be seen that the orbit is indeed the mirror image of that pictured in Fig. 32.
Figure 33:
Equally spaced (in time) points on a time-asymptotic orbit in phase-space. Data
calculated numerically for 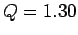 ,
, 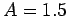 ,
, 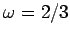 ,
, 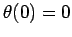 ,
,
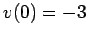 , and
, and
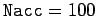 .
.
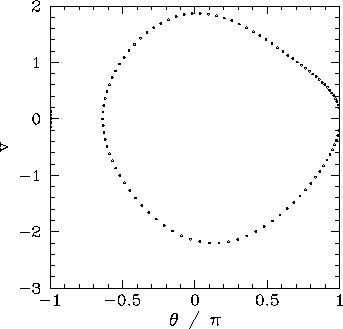 |
Figure 34 shows the 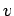 -coordinate of the Poincaré section of a time-asymptotic orbit,
calculated with the same physics parameters used in Fig. 30, versus
-coordinate of the Poincaré section of a time-asymptotic orbit,
calculated with the same physics parameters used in Fig. 30, versus
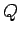 in the range
in the range 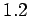 and
and 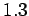 . Data is shown for the two sets of
initial conditions discussed above. The figure is interpreted as
follows. When
. Data is shown for the two sets of
initial conditions discussed above. The figure is interpreted as
follows. When 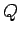 is less than a critical value,
which is about
is less than a critical value,
which is about 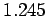 , then the two sets of initial conditions lead to motions
which converge on the same, left-right symmetric,
period-1 attractor. However, once
, then the two sets of initial conditions lead to motions
which converge on the same, left-right symmetric,
period-1 attractor. However, once
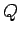 exceeds the critical value then the attractor bifurcates into two
asymmetric, mirror image, period-1
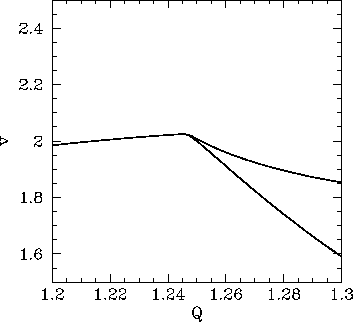
attractors. Obviously, the bifurcation is indicated by the forking of the
curve shown in Fig. 34. The lower and upper branches correspond to the left- and right-favouring
attractors, respectively.
exceeds the critical value then the attractor bifurcates into two
asymmetric, mirror image, period-1
attractors. Obviously, the bifurcation is indicated by the forking of the
curve shown in Fig. 34. The lower and upper branches correspond to the left- and right-favouring
attractors, respectively.
Figure 34:
The 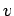 -coordinate of the Poincaré section of a time-asymptotic orbit
plotted against the quality-factor
-coordinate of the Poincaré section of a time-asymptotic orbit
plotted against the quality-factor 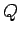 . Data
calculated numerically for
. Data
calculated numerically for
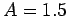 ,
, 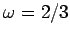 , and
, and
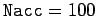 . Data is shown for two sets of initial
conditions:
. Data is shown for two sets of initial
conditions: 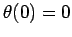 and
and 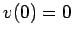 (lower branch); and
(lower branch); and 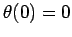 and
and 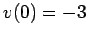 (upper branch).
(upper branch).
 |
Spontaneous symmetry breaking, which is the fundamental non-linear process illustrated in the
above discussion, plays an
important role in many areas of physics. For instance, symmetry breaking gives mass
to elementary particles in the unified theory of electromagnetic and weak interactions.25Symmetry breaking also plays a pivotal role in the so-called ``inflation'' theory of the expansion
of the early universe.26



Next: Basins of attraction
Up: The chaotic pendulum
Previous: The Poincaré section
Richard Fitzpatrick
2006-03-29




![]() ,
, ![]() , and
, and ![]() fixed, but change the initial conditions
fixed, but change the initial conditions ![]() and
and ![]() . Figure 33 shows
a time-asymptotic phase-space orbit calculated with the same physics parameters used in Fig. 32, but
with the initial conditions
. Figure 33 shows
a time-asymptotic phase-space orbit calculated with the same physics parameters used in Fig. 32, but
with the initial conditions ![]() and
and ![]() , instead of
, instead of ![]() and
and
![]() . It can be seen that the orbit is indeed the mirror image of that pictured in Fig. 32.
. It can be seen that the orbit is indeed the mirror image of that pictured in Fig. 32.

![]() -coordinate of the Poincaré section of a time-asymptotic orbit,
calculated with the same physics parameters used in Fig. 30, versus
-coordinate of the Poincaré section of a time-asymptotic orbit,
calculated with the same physics parameters used in Fig. 30, versus
![]() in the range
in the range ![]() and
and ![]() . Data is shown for the two sets of
initial conditions discussed above. The figure is interpreted as
follows. When
. Data is shown for the two sets of
initial conditions discussed above. The figure is interpreted as
follows. When ![]() is less than a critical value,
which is about
is less than a critical value,
which is about ![]() , then the two sets of initial conditions lead to motions
which converge on the same, left-right symmetric,
period-1 attractor. However, once
, then the two sets of initial conditions lead to motions
which converge on the same, left-right symmetric,
period-1 attractor. However, once
![]() exceeds the critical value then the attractor bifurcates into two
asymmetric, mirror image, period-1
attractors. Obviously, the bifurcation is indicated by the forking of the
curve shown in Fig. 34. The lower and upper branches correspond to the left- and right-favouring
attractors, respectively.
exceeds the critical value then the attractor bifurcates into two
asymmetric, mirror image, period-1
attractors. Obviously, the bifurcation is indicated by the forking of the
curve shown in Fig. 34. The lower and upper branches correspond to the left- and right-favouring
attractors, respectively.
