| (33) | |||
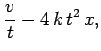 |
(34) |
| (33) | |||
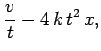 |
(34) |
| (35) |
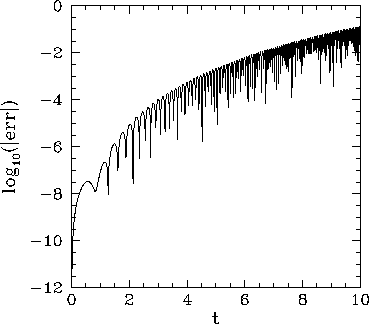 |
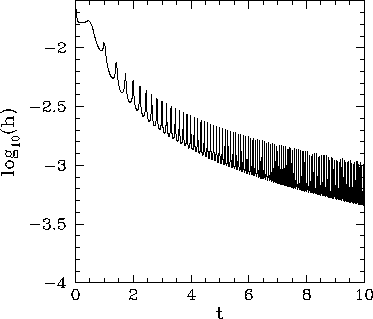
Let us compare the above solution with that obtained numerically using
a fourth-order Runge-Kutta method. Figure 7 shows the integration error
associated with such a method (calculated by integrating the above system, with ![]() ,
from
,
from ![]() to
to ![]() , and then taking the difference between the numerical and analytic
solutions) with a fixed step-length of
, and then taking the difference between the numerical and analytic
solutions) with a fixed step-length of ![]() , plotted against the independent variable,
, plotted against the independent variable, ![]() .
It can be seen that, although the error starts off small, it rises rapidly as the
variation scale-length of the solution decreases (i.e., as
.
It can be seen that, although the error starts off small, it rises rapidly as the
variation scale-length of the solution decreases (i.e., as ![]() increases), and
quickly becomes unacceptably large. Of course, we could reduce the error by simply reducing
the step-length,
increases), and
quickly becomes unacceptably large. Of course, we could reduce the error by simply reducing
the step-length, ![]() . However, this is a very inefficient solution. The step-length
only needs to be reduced at large
. However, this is a very inefficient solution. The step-length
only needs to be reduced at large ![]() . There is no need to reduce it, at all, at small
. There is no need to reduce it, at all, at small ![]() .
Clearly, the ideal solution to this problem would be an integration method in which
the step-length is varied so as to maintain a relatively constant truncation error
per step. Such an adaptive integration method would take large steps when variation
scale-length of the solution was large, and vice versa.
.
Clearly, the ideal solution to this problem would be an integration method in which
the step-length is varied so as to maintain a relatively constant truncation error
per step. Such an adaptive integration method would take large steps when variation
scale-length of the solution was large, and vice versa.
Let us investigate how we could convert our fixed step-length, fourth-order Runge-Kutta
method into a corresponding adaptive method. First of all, we need an estimate of the
truncation error at each step. Suppose that the current step-length is ![]() . We can
estimate the truncation error,
. We can
estimate the truncation error, ![]() , associated with
the current step by taking the difference between the solutions obtained by stepping
by
, associated with
the current step by taking the difference between the solutions obtained by stepping
by ![]() twice and by
twice and by ![]() once (starting from the same point,
in both cases). Let
once (starting from the same point,
in both cases). Let ![]() be the desired truncation
error per step. How do we adjust
be the desired truncation
error per step. How do we adjust ![]() so as to ensure that the truncation error
associated with the next step is closer to this value? Observe, from Eq. (29),
that the truncation error per step in a fourth-order scheme scales like
so as to ensure that the truncation error
associated with the next step is closer to this value? Observe, from Eq. (29),
that the truncation error per step in a fourth-order scheme scales like ![]() . It
follows, therefore, that our step-length adjustment formula should take the form16
. It
follows, therefore, that our step-length adjustment formula should take the form16
| (36) |
There are a number of caveats to the above discussion. In a system of ![]() coupled
o.d.e.s, the overall truncation error per step,
coupled
o.d.e.s, the overall truncation error per step, ![]() , should, of course, be some appropriately
weighted average of the errors associated with each equation. There is also a question
of whether
, should, of course, be some appropriately
weighted average of the errors associated with each equation. There is also a question
of whether ![]() should be an absolute error or a relative error. The
relative error associated with the
should be an absolute error or a relative error. The
relative error associated with the ![]() th equation is simply the absolute error
divided by
th equation is simply the absolute error
divided by ![]() , where
, where ![]() is the current value of the
is the current value of the ![]() th dependent variable.
An absolute error estimate is appropriate to a system of equations in which the amplitudes
of the various dependent variables remain bounded. A relative error estimate
is appropriate to a system in which the amplitudes of the dependent variables blow-up at some point, but
the variables always
remain the same sign. Finally, a mixed error estimate--usually the minimum of the
absolute and relative errors--is appropriate to a system in which the amplitudes of the dependent variables blow-up at some point, but
the signs of the variables oscillate. It is usually a good idea to place some
limits on the allowed variation of the step-length from step to step: e.g., by preventing
the step-length from increasing or decreasing by more than some factor
th dependent variable.
An absolute error estimate is appropriate to a system of equations in which the amplitudes
of the various dependent variables remain bounded. A relative error estimate
is appropriate to a system in which the amplitudes of the dependent variables blow-up at some point, but
the variables always
remain the same sign. Finally, a mixed error estimate--usually the minimum of the
absolute and relative errors--is appropriate to a system in which the amplitudes of the dependent variables blow-up at some point, but
the signs of the variables oscillate. It is usually a good idea to place some
limits on the allowed variation of the step-length from step to step: e.g., by preventing
the step-length from increasing or decreasing by more than some factor ![]() per step. This
prevents
per step. This
prevents ![]() from oscillating unduly about its optimum value. Obviously, if
from oscillating unduly about its optimum value. Obviously, if ![]() becomes
absurdly small then the integration method has failed, and should abort with an
appropriate error message. Finally, a limit should be placed on how
large
becomes
absurdly small then the integration method has failed, and should abort with an
appropriate error message. Finally, a limit should be placed on how
large ![]() can become--unfortunately, adaptive methods have a tendency to become a little
over optimistic when integration is easy.
can become--unfortunately, adaptive methods have a tendency to become a little
over optimistic when integration is easy.
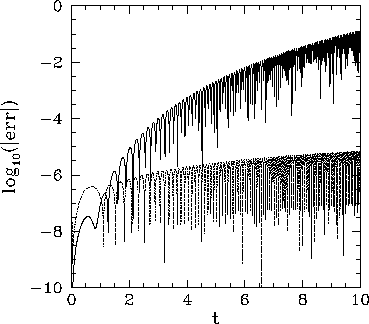 |
Figure 8 shows the integration errors
associated with a fixed step-length, fourth-order Runge-Kutta
method and a corresponding adaptive method--constructed
along the lines discussed above--as functions of
the independent variable, ![]() . The errors are
calculated by integrating the current system, with
. The errors are
calculated by integrating the current system, with ![]() ,
from
,
from ![]() to
to ![]() , and then taking the difference between the numerical and analytic
solutions. The fixed step-length associated with the former method is
, and then taking the difference between the numerical and analytic
solutions. The fixed step-length associated with the former method is ![]() . The desired
truncation error per step associated with the latter is
. The desired
truncation error per step associated with the latter is
![]() . It
can be seen that the performance of the adaptive method is far
superior to that of the fixed step-length method, since the former method
maintains a relatively constant integration error as the variation scale-length
of the solution decreases (i.e., as
. It
can be seen that the performance of the adaptive method is far
superior to that of the fixed step-length method, since the former method
maintains a relatively constant integration error as the variation scale-length
of the solution decreases (i.e., as ![]() increases). Figure 9 illustrates how this is achieved.
This figure shows the step-length,
increases). Figure 9 illustrates how this is achieved.
This figure shows the step-length, ![]() , associated with the adaptive method as a function of
, associated with the adaptive method as a function of ![]() .
It can be seen that the adaptive method maintains a relatively constant
truncation error per step by decreasing
.
It can be seen that the adaptive method maintains a relatively constant
truncation error per step by decreasing
![]() as
as ![]() increases.
increases.
 |