


Next: Adaptive integration methods
Up: Integration of ODEs
Previous: An example fixed-step RK4
Consider the following system of o.d.e.s:
subject to the initial conditions 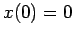 and
and
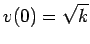 at
at 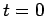 . In fact,
this system can be solved analytically to give
. In fact,
this system can be solved analytically to give
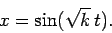 |
(32) |
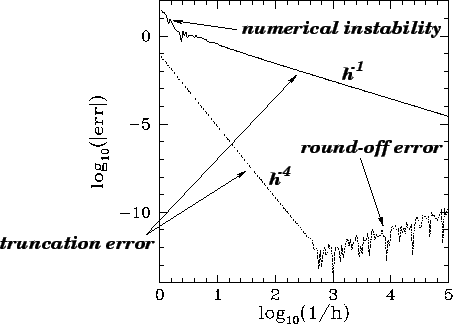
Let us compare the above solution with that obtained numerically using either Euler's method
or a fourth-order Runge-Kutta method. Figure 5 shows the integration errors
associated with these two methods (calculated by integrating the above system, with 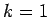 ,
from
,
from 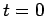 to
to 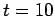 , and then taking the difference between the numerical and analytic
solutions) plotted against the step-length,
, and then taking the difference between the numerical and analytic
solutions) plotted against the step-length, 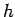 , in a log-log graph. All calculations
are performed to single precision: i.e., by using float, rather
than double, variables. It can be seen that at large values of
, in a log-log graph. All calculations
are performed to single precision: i.e., by using float, rather
than double, variables. It can be seen that at large values of 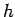 , the error associated
with Euler's method becomes much greater than unity (i.e., the magnitude of the
numerical solution greatly exceeds that of the analytic solution), indicating the
presence of a numerical instability. There are no similar signs of instability
associated with the Runge-Kutta method. At intermediate
, the error associated
with Euler's method becomes much greater than unity (i.e., the magnitude of the
numerical solution greatly exceeds that of the analytic solution), indicating the
presence of a numerical instability. There are no similar signs of instability
associated with the Runge-Kutta method. At intermediate 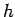 , the
error associated with Euler's method decreases smoothly like
, the
error associated with Euler's method decreases smoothly like 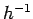 : in this regime, the
dominant error is truncation error, which is expected to scale like
: in this regime, the
dominant error is truncation error, which is expected to scale like 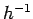 for a first-order
method. The error associated with the Runge-Kutta method similarly scales like
for a first-order
method. The error associated with the Runge-Kutta method similarly scales like 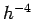 --as
expected for a fourth-order scheme--in the
truncation error dominated regime. Note that, as
--as
expected for a fourth-order scheme--in the
truncation error dominated regime. Note that, as 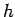 is decreased, the error associated with both
methods eventually starts to rise in a jagged curve that scales roughly like
is decreased, the error associated with both
methods eventually starts to rise in a jagged curve that scales roughly like 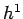 . This
is a manifestation of round-off error. The minimum error associated with both methods
corresponds to the boundary between the truncation error and round-off error dominated
regimes. Thus, for Euler's method the minimum error is about
. This
is a manifestation of round-off error. The minimum error associated with both methods
corresponds to the boundary between the truncation error and round-off error dominated
regimes. Thus, for Euler's method the minimum error is about 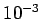 at
at 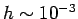 ,
whereas for the Runge-Kutta method the minimum error is about
,
whereas for the Runge-Kutta method the minimum error is about 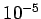 at
at 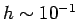 .
Clearly, the performance of the Runge-Kutta method is vastly superior to that of Euler's method,
since the former method is capable of attaining much greater accuracy than the latter
using a far smaller number
of steps (i.e., a far larger
.
Clearly, the performance of the Runge-Kutta method is vastly superior to that of Euler's method,
since the former method is capable of attaining much greater accuracy than the latter
using a far smaller number
of steps (i.e., a far larger 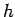 ).
).
Figure 5:
Global integration errors associated with Euler's method (solid curve) and a
fourth-order Runge-Kutta method (dotted curve) plotted
against the step-length 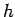 . Single precision calculation.
. Single precision calculation.
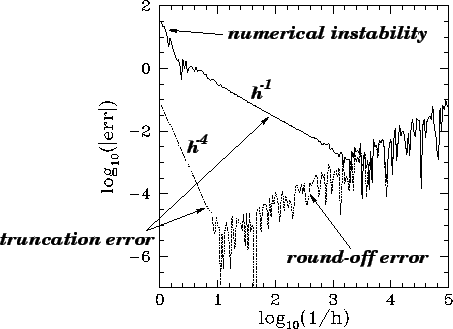 |
Figure 6 displays similar data to that shown in Fig. 5, except that now all
of the calculations
are performed to double precision. The figure exhibits the same broad features as
those apparent in Fig. 5. The major difference is that the round-off error has
been reduced by about nine orders of magnitude, allowing the Runge-Kutta method to
attain a minimum error of about 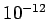 (see Tab. 1)--a remarkably performance!
(see Tab. 1)--a remarkably performance!
Figure 6:
Global integration errors associated with Euler's method (solid curve) and a
fourth-order Runge-Kutta method (dotted curve) plotted
against the step-length 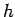 . Double precision calculation.
. Double precision calculation.
 |
Figures 5 and 6 illustrate why scientists rarely use Euler's method, or single
precision numerics, to integrate systems of o.d.e.s.



Next: Adaptive integration methods
Up: Integration of ODEs
Previous: An example fixed-step RK4
Richard Fitzpatrick
2006-03-29

![]() (see Tab. 1)--a remarkably performance!
(see Tab. 1)--a remarkably performance!
