


Next: Numerical errors
Up: Integration of ODEs
Previous: Introduction
Consider the general first-order o.d.e.,
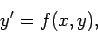 |
(5) |
where  denotes
denotes 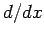 , subject to the general initial-value boundary
condition
, subject to the general initial-value boundary
condition
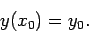 |
(6) |
Clearly, if we can find a method for numerically solving this problem, then we should
have little difficulty generalizing it to
deal with a system of 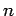 simultaneous first-order o.d.e.s.
simultaneous first-order o.d.e.s.
It is important to appreciate that the numerical solution to a differential
equation is only an approximation to the actual solution. The actual
solution, 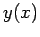 , to Eq. (5) is (presumably)
a continuous function of a continuous
variable,
, to Eq. (5) is (presumably)
a continuous function of a continuous
variable,  . However, when we solve this equation numerically, the best that we can
do is to evaluate approximations to the
function
. However, when we solve this equation numerically, the best that we can
do is to evaluate approximations to the
function 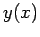 at a series of discrete grid-points, the
at a series of discrete grid-points, the 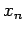 (say), where
(say), where
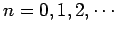 and
and
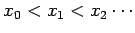 . For the moment, we shall restrict our
discussion to equally spaced grid-points, where
. For the moment, we shall restrict our
discussion to equally spaced grid-points, where
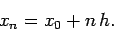 |
(7) |
Here, the quantity 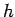 is referred to as the step-length.
Let
is referred to as the step-length.
Let 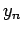 be our approximation
to
be our approximation
to 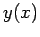 at the grid-point
at the grid-point 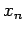 . A numerical integration scheme is
essentially a method which somehow employs the information contained in the original
o.d.e., Eq. (5), to construct a series of rules interrelating the
various
. A numerical integration scheme is
essentially a method which somehow employs the information contained in the original
o.d.e., Eq. (5), to construct a series of rules interrelating the
various 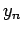 .
.
The simplest possible integration scheme was invented by the celebrated
18th century Swiss mathematician Leonhard Euler, and is, therefore, called
Euler's method. Incidentally, it is interesting to note that virtually
all of the standard methods used in numerical analysis were invented
before the advent of electronic computers. In olden days, people
actually performed numerical calculations by hand--and a very long and tedious
process it must have been! Suppose that we have evaluated
an approximation, 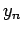 , to the solution,
, to the solution, 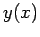 , of Eq. (5) at the grid-point
, of Eq. (5) at the grid-point
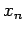 . The approximate gradient of
. The approximate gradient of 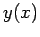 at this point is, therefore, given by
at this point is, therefore, given by
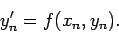 |
(8) |
Let us approximate the curve 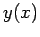 as a straight-line between the
neighbouring grid-points
as a straight-line between the
neighbouring grid-points 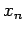 and
and 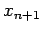 . It follows that
. It follows that
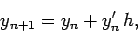 |
(9) |
or
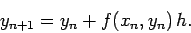 |
(10) |
The above formula is the essence of Euler's method. It enables us to calculate
all of the 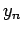 , given the initial value,
, given the initial value, 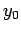 , at the first grid-point,
, at the first grid-point,
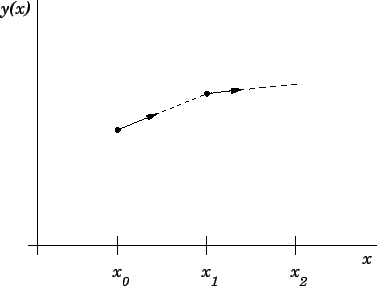
 . Euler's method is illustrated in Fig. 4.
. Euler's method is illustrated in Fig. 4.
Figure 4:
Illustration of Euler's method.
 |



Next: Numerical errors
Up: Integration of ODEs
Previous: Introduction
Richard Fitzpatrick
2006-03-29
![]() , to Eq. (5) is (presumably)
a continuous function of a continuous
variable,
, to Eq. (5) is (presumably)
a continuous function of a continuous
variable, ![]() . However, when we solve this equation numerically, the best that we can
do is to evaluate approximations to the
function
. However, when we solve this equation numerically, the best that we can
do is to evaluate approximations to the
function ![]() at a series of discrete grid-points, the
at a series of discrete grid-points, the ![]() (say), where
(say), where
![]() and
and
![]() . For the moment, we shall restrict our
discussion to equally spaced grid-points, where
. For the moment, we shall restrict our
discussion to equally spaced grid-points, where
![]() , to the solution,
, to the solution, ![]() , of Eq. (5) at the grid-point
, of Eq. (5) at the grid-point
![]() . The approximate gradient of
. The approximate gradient of ![]() at this point is, therefore, given by
at this point is, therefore, given by