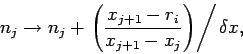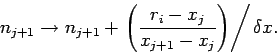Next: Solution of Poisson's equation
Up: Particle-in-cell codes
Previous: Solution of electron equations
In order to obtain the electron number density 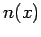 from the electron coordinates
from the electron coordinates 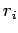 we adopt a so-called particle-in-cell (PIC) approach.
Let us define a set of
we adopt a so-called particle-in-cell (PIC) approach.
Let us define a set of 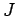 equally
spaced spatial grid-points located at coordinates
equally
spaced spatial grid-points located at coordinates
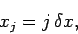 |
(300) |
for 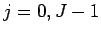 , where
, where
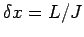 . Let
. Let
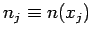 .
Suppose that the
.
Suppose that the 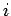 th electron lies between the
th electron lies between the 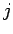 th and
th and 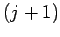 th grid-points:
i.e.,
th grid-points:
i.e.,
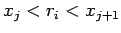 . We let
. We let
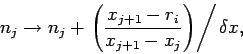 |
(301) |
and
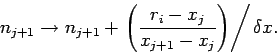 |
(302) |
Thus, 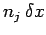 increases by 1 if the electron is at the
increases by 1 if the electron is at the 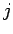 th grid-point,
th grid-point,
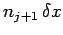 increases by 1 if the electron is at the
increases by 1 if the electron is at the 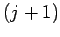 th grid-point, and
th grid-point, and 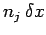 and
and
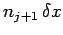 both increase by
both increase by 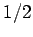 if the electron is halfway between the two grid-points, etc.
Performing a similar assignment for each electron in turn allows us to
build up the
if the electron is halfway between the two grid-points, etc.
Performing a similar assignment for each electron in turn allows us to
build up the 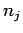 from the electron coordinates (assuming that all the
from the electron coordinates (assuming that all the 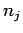 are initialized
to zero at the start of this process).
are initialized
to zero at the start of this process).



Next: Solution of Poisson's equation
Up: Particle-in-cell codes
Previous: Solution of electron equations
Richard Fitzpatrick
2006-03-29