Suppose that the opaque screen in our interference/diffraction apparatus contains 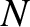 identical, equally spaced, parallel slits of finite width. Let the slit spacing be
identical, equally spaced, parallel slits of finite width. Let the slit spacing be 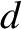 , and the
slit width
, and the
slit width 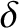 , where
, where
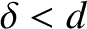 . It follows that the aperture function for the screen is written
. It follows that the aperture function for the screen is written
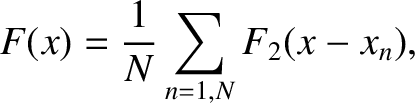 |
(10.59) |
where
![$\displaystyle x_n = [n-(N+1)/2]\,d,$](img3453.png) |
(10.60) |
and
![\begin{displaymath}F_2(x)=\left\{
\begin{array}{ccc}
1/\delta&\mbox{\hspace{0.5c...
...elta/2\\ [0.5ex]
0 &&\vert x\vert> \delta/2
\end{array}\right..\end{displaymath}](img3454.png) |
(10.61) |
We recognize 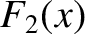 as the aperture function for a single slit, of finite width
as the aperture function for a single slit, of finite width 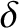 , that is centered on
, that is centered on 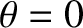 . [See Equation (10.54).]
. [See Equation (10.54).]
Assuming normal incidence (i.e.,
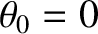 ), the interference/diffraction function, which is the Fourier transform
of the aperture function, takes the form [see Equation (10.52)]
), the interference/diffraction function, which is the Fourier transform
of the aperture function, takes the form [see Equation (10.52)]
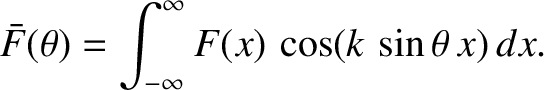 |
(10.62) |
Hence,
where 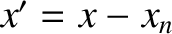 . Here, we have made use of the result
. Here, we have made use of the result
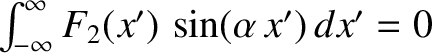 , for any
, for any 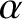 ,
which follows because
,
which follows because 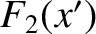 is even in
is even in 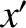 , whereas
, whereas
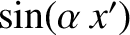 is odd.
We have also employed the trigonometric identity
is odd.
We have also employed the trigonometric identity
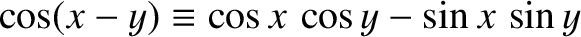 . (See Appendix B.)
The previous expression reduces to
. (See Appendix B.)
The previous expression reduces to
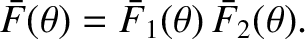 |
(10.64) |
Here [cf., Equation (10.38)],
![$\displaystyle \bar{F}_1(\theta)= \int_{-\infty}^\infty F_1(x)\,\cos(k\,\sin\the...
...ac{\sin[\pi\,N\,(d/\lambda)\,\sin\theta]}{\sin [\pi\,(d/\lambda)\,\sin\theta]},$](img3470.png) |
(10.65) |
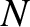 identical parallel slits of negligible width that are equally spaced a distance
identical parallel slits of negligible width that are equally spaced a distance 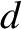 apart, and
apart, and
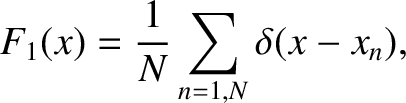 |
(10.66) |
is the corresponding aperture function.
Furthermore [cf., Equation (10.55)],
![$\displaystyle \bar{F}_2(\theta) = \int_{-\infty}^\infty F_2(x)\,\cos(k\,\sin\theta\,x)\,dx = {\rm sinc}\left[\pi\,\frac{\delta}{\lambda}\,\sin\theta\right],$](img3472.png) |
(10.67) |
is the interference/diffraction function for a single slit of width 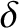 .
.
Figure 10.12:
Multi-slit far-field interference pattern calculated for 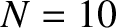 ,
,
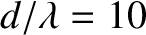 , and
, and
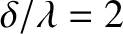 , assuming normal
incidence.
, assuming normal
incidence.
|
|
We conclude, from the preceding analysis, that the interference/diffraction function for 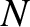 identical, equally spaced, parallel slits of
finite width is the product of the interference/diffraction function for
identical, equally spaced, parallel slits of
finite width is the product of the interference/diffraction function for 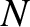 identical, equally spaced, parallel slits of
negligible width,
identical, equally spaced, parallel slits of
negligible width,
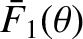 , and the interference/diffraction function for a single slit of finite width,
, and the interference/diffraction function for a single slit of finite width,
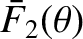 .
We have already encountered both of these functions. The former function (see Figure 10.8, which shows
.
We have already encountered both of these functions. The former function (see Figure 10.8, which shows
![$[\bar{F}_1(\theta)]^{\,2}$](img3476.png) ) consists of a series of sharp maxima of equal amplitude located
at [see Equation (10.39)]
) consists of a series of sharp maxima of equal amplitude located
at [see Equation (10.39)]
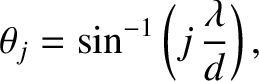 |
(10.68) |
where 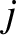 is an integer. The latter function (see Figure 10.10, which shows
is an integer. The latter function (see Figure 10.10, which shows
![$[\bar{F}_2(\theta-\theta_0)]^{\,2}$](img3478.png) ) is of order unity for
) is of order unity for
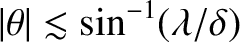 , and much less than unity for
, and much less than unity for
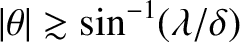 .
It follows that the interference/diffraction pattern associated with
.
It follows that the interference/diffraction pattern associated with 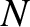 identical, equally spaced, parallel slits of finite width, which is given by
identical, equally spaced, parallel slits of finite width, which is given by
![$\displaystyle {\cal I}(\theta) \propto \left[\bar{F}_1(\theta)\,\bar{F}_2(\thet...
...pto\left[\bar{F}_1(\theta)\right]^{\,2}\, \left[\bar{F}_2(\theta)\right]^{\,2},$](img3481.png) |
(10.69) |
is similar to that for 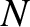 identical, equally spaced, parallel slits of negligible width,
identical, equally spaced, parallel slits of negligible width,
![$[\bar{F}_1(\theta)]^{\,2}$](img3476.png) , except that the intensities of the various maxima in the pattern are
modulated by
, except that the intensities of the various maxima in the pattern are
modulated by
![$[\bar{F}_2(\theta)]^{\,2}$](img3482.png) .
Hence, those maxima lying in the angular range
.
Hence, those maxima lying in the angular range
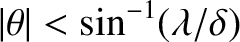 are of similar intensity, whereas those lying in the range
are of similar intensity, whereas those lying in the range
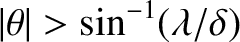 are of negligible intensity. This is illustrated in Figure 10.12, which shows the multi-slit interference/diffraction
pattern calculated for
are of negligible intensity. This is illustrated in Figure 10.12, which shows the multi-slit interference/diffraction
pattern calculated for 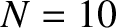 ,
,
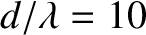 , and
, and
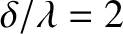 . As expected, the maxima lying
in the angular range
. As expected, the maxima lying
in the angular range
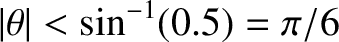 have relatively large
intensities, whereas those lying in the
range
have relatively large
intensities, whereas those lying in the
range
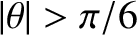 have negligibly small intensities.
have negligibly small intensities.
 identical, equally spaced, parallel slits of finite width. Let the slit spacing be
identical, equally spaced, parallel slits of finite width. Let the slit spacing be 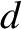 , and the
slit width
, and the
slit width 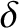 , where
, where
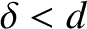 . It follows that the aperture function for the screen is written
. It follows that the aperture function for the screen is written
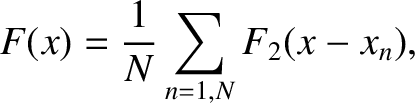
![$\displaystyle x_n = [n-(N+1)/2]\,d,$](img3453.png)
![\begin{displaymath}F_2(x)=\left\{
\begin{array}{ccc}
1/\delta&\mbox{\hspace{0.5c...
...elta/2\\ [0.5ex]
0 &&\vert x\vert> \delta/2
\end{array}\right..\end{displaymath}](img3454.png)
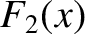 as the aperture function for a single slit, of finite width
as the aperture function for a single slit, of finite width 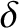 , that is centered on
, that is centered on 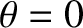 . [See Equation (10.54).]
. [See Equation (10.54).]
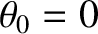 ), the interference/diffraction function, which is the Fourier transform
of the aperture function, takes the form [see Equation (10.52)]
), the interference/diffraction function, which is the Fourier transform
of the aperture function, takes the form [see Equation (10.52)]
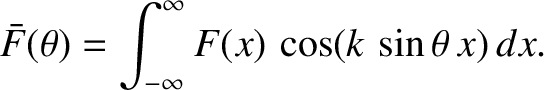
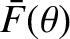
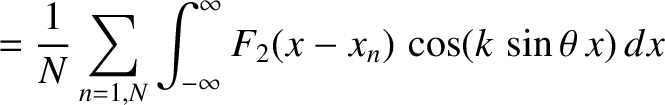
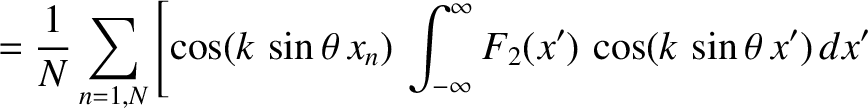
![$\displaystyle ~~~~\left.
- \sin(k\,\sin\theta\,x_n)\,\int_{-\infty}^\infty F_2(x')\,\sin(k\,\sin\theta\,x')\,dx'\right]$](img3461.png)
![$\displaystyle =\left[\frac{1}{N}\sum_{n=1,N} \cos(k\,\sin\theta\,x_n)\right] \int_{-\infty}^\infty F_2(x')\,\cos(k\,\sin\theta\,x')\,dx',$](img3462.png)
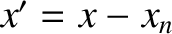 . Here, we have made use of the result
. Here, we have made use of the result
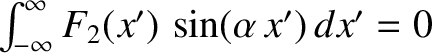 , for any
, for any  ,
which follows because
,
which follows because  is even in
is even in  , whereas
, whereas
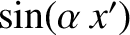 is odd.
We have also employed the trigonometric identity
is odd.
We have also employed the trigonometric identity
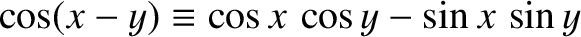 . (See Appendix B.)
The previous expression reduces to
. (See Appendix B.)
The previous expression reduces to
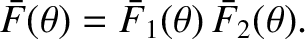
![$\displaystyle \bar{F}_1(\theta)= \int_{-\infty}^\infty F_1(x)\,\cos(k\,\sin\the...
...ac{\sin[\pi\,N\,(d/\lambda)\,\sin\theta]}{\sin [\pi\,(d/\lambda)\,\sin\theta]},$](img3470.png)
 identical parallel slits of negligible width that are equally spaced a distance
identical parallel slits of negligible width that are equally spaced a distance 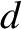 apart, and
apart, and
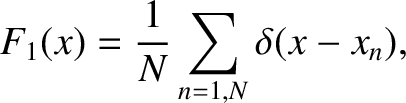
![$\displaystyle \bar{F}_2(\theta) = \int_{-\infty}^\infty F_2(x)\,\cos(k\,\sin\theta\,x)\,dx = {\rm sinc}\left[\pi\,\frac{\delta}{\lambda}\,\sin\theta\right],$](img3472.png)
 .
.
![\includegraphics[width=0.9\textwidth]{Chapter10/fig10_12.eps}](img3473.png)
 identical, equally spaced, parallel slits of
finite width is the product of the interference/diffraction function for
identical, equally spaced, parallel slits of
finite width is the product of the interference/diffraction function for 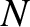 identical, equally spaced, parallel slits of
negligible width,
identical, equally spaced, parallel slits of
negligible width,
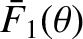 , and the interference/diffraction function for a single slit of finite width,
, and the interference/diffraction function for a single slit of finite width,
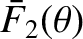 .
We have already encountered both of these functions. The former function (see Figure 10.8, which shows
.
We have already encountered both of these functions. The former function (see Figure 10.8, which shows
![$[\bar{F}_1(\theta)]^{\,2}$](img3476.png) ) consists of a series of sharp maxima of equal amplitude located
at [see Equation (10.39)]
) consists of a series of sharp maxima of equal amplitude located
at [see Equation (10.39)]
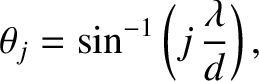
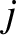 is an integer. The latter function (see Figure 10.10, which shows
is an integer. The latter function (see Figure 10.10, which shows
![$[\bar{F}_2(\theta-\theta_0)]^{\,2}$](img3478.png) ) is of order unity for
) is of order unity for
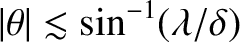 , and much less than unity for
, and much less than unity for
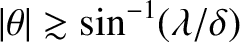 .
It follows that the interference/diffraction pattern associated with
.
It follows that the interference/diffraction pattern associated with  identical, equally spaced, parallel slits of finite width, which is given by
identical, equally spaced, parallel slits of finite width, which is given by
![$\displaystyle {\cal I}(\theta) \propto \left[\bar{F}_1(\theta)\,\bar{F}_2(\thet...
...pto\left[\bar{F}_1(\theta)\right]^{\,2}\, \left[\bar{F}_2(\theta)\right]^{\,2},$](img3481.png)
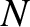 identical, equally spaced, parallel slits of negligible width,
identical, equally spaced, parallel slits of negligible width,
![$[\bar{F}_1(\theta)]^{\,2}$](img3476.png) , except that the intensities of the various maxima in the pattern are
modulated by
, except that the intensities of the various maxima in the pattern are
modulated by
![$[\bar{F}_2(\theta)]^{\,2}$](img3482.png) .
Hence, those maxima lying in the angular range
.
Hence, those maxima lying in the angular range
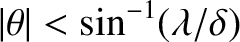 are of similar intensity, whereas those lying in the range
are of similar intensity, whereas those lying in the range
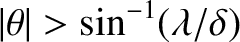 are of negligible intensity. This is illustrated in Figure 10.12, which shows the multi-slit interference/diffraction
pattern calculated for
are of negligible intensity. This is illustrated in Figure 10.12, which shows the multi-slit interference/diffraction
pattern calculated for 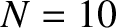 ,
,
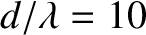 , and
, and
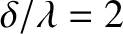 . As expected, the maxima lying
in the angular range
. As expected, the maxima lying
in the angular range
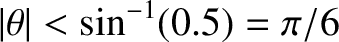 have relatively large
intensities, whereas those lying in the
range
have relatively large
intensities, whereas those lying in the
range
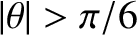 have negligibly small intensities.
have negligibly small intensities.