Next: Longitudinal Standing Waves Up: Transverse Standing Waves Previous: General Time Evolution of Contents
 beads that is similar
to that pictured in Figure 4.1, except that each end of the string
is attached to a massless ring that slides (in the
beads that is similar
to that pictured in Figure 4.1, except that each end of the string
is attached to a massless ring that slides (in the  -direction)
on a frictionless rod.
-direction)
on a frictionless rod.
![$\displaystyle y_{n,i}(t) = A_n\,\cos\left[\frac{n\,(i-1/2)}{N}\,\pi\right]\,\cos(\omega_n\,t-\phi_n),
$](img1072.png)
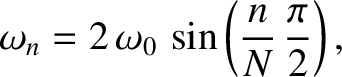
 is as defined in Section 4.2,
is as defined in Section 4.2, 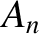 and
and 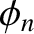 are constants, the integer
are constants, the integer 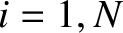 indexes the beads, and the mode number
indexes the beads, and the mode number  indexes the
modes.
indexes the
modes.
 beads that is similar
to that pictured in Figure 4.1, except that the left end of the string is
fixed, and the right end is attached to a massless ring which slides (in the
beads that is similar
to that pictured in Figure 4.1, except that the left end of the string is
fixed, and the right end is attached to a massless ring which slides (in the  -direction)
on a frictionless rod. Find the normal
modes and normal frequencies of the system.
-direction)
on a frictionless rod. Find the normal
modes and normal frequencies of the system.
 identical inductors of inductance
identical inductors of inductance 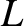 , and
, and 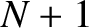 identical capacitors of capacitance
identical capacitors of capacitance  . Let the instantaneous current
flowing through the
. Let the instantaneous current
flowing through the 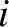 th inductor be
th inductor be 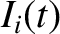 , for
, for 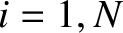 . Demonstrate from
Kirchhoff's circuital laws that the currents evolve in time according to the
coupled equations
. Demonstrate from
Kirchhoff's circuital laws that the currents evolve in time according to the
coupled equations
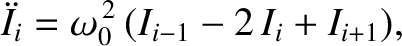
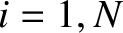 , where
, where
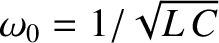 , and
, and
 .
Find the normal frequencies of the system.
.
Find the normal frequencies of the system.
 , tension
, tension  , and mass per unit length
, and mass per unit length
 , is stretched between two immovable walls. Suppose that the string is
initially in its equilibrium state. At
, is stretched between two immovable walls. Suppose that the string is
initially in its equilibrium state. At  it is
struck by a hammer in such a manner as to impart an impulsive
velocity
it is
struck by a hammer in such a manner as to impart an impulsive
velocity 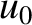 to a small segment of length
to a small segment of length 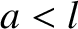 centered on the mid-point.
Find an expression for the subsequent motion of the string. Plot the motion
as a function of time in a similar fashion to Figure 4.11, assuming that
centered on the mid-point.
Find an expression for the subsequent motion of the string. Plot the motion
as a function of time in a similar fashion to Figure 4.11, assuming that
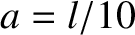 .
.
 , tension
, tension  , and mass per unit length
, and mass per unit length
 , is stretched between two massless rings, attached to its ends, that
slide (in the
, is stretched between two massless rings, attached to its ends, that
slide (in the  -direction) along frictionless rods.
-direction) along frictionless rods.
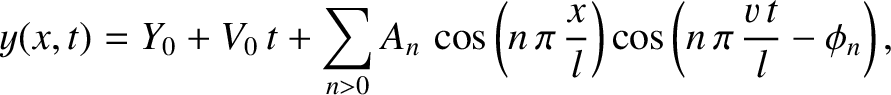
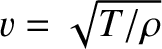 , and
, and 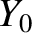 ,
, 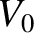 ,
, 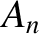 , and
, and 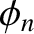 are arbitrary constants.
are arbitrary constants.
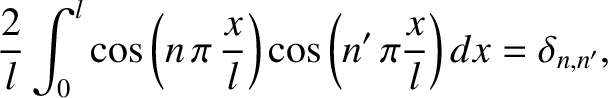
 and
and 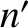 are integers (that are not both zero).
are integers (that are not both zero).
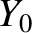 |
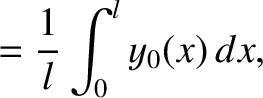 |
|
 |
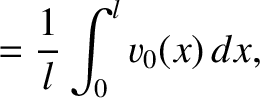 |
|
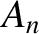 |
 |
|
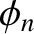 |
 |
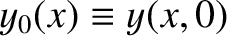 ,
,
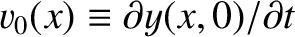 , and
, and
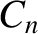 |
 |
|
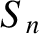 |
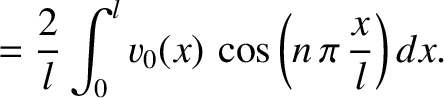 |
 it is
struck by a hammer in such a manner as to impart an impulsive
velocity
it is
struck by a hammer in such a manner as to impart an impulsive
velocity 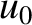 to a small segment of length
to a small segment of length 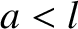 centered on the mid-point.
Find an expression for the subsequent motion of the string.
centered on the mid-point.
Find an expression for the subsequent motion of the string.
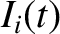 represents
represents 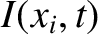 , where
, where
 . Moreover,
. Moreover,
 , and
, and
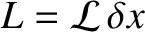 , where
, where  and
and 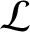 are the capacitance per unit length and the
inductance per unit length of the line, respectively.
are the capacitance per unit length and the
inductance per unit length of the line, respectively.
 ,
the evolution equation for the coupled currents given in Exercise 3 reduces to
the wave equation
,
the evolution equation for the coupled currents given in Exercise 3 reduces to
the wave equation
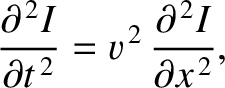
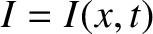 ,
,  measures distance along the line, and
measures distance along the line, and
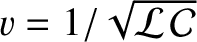 .
.
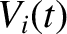 is the potential difference (measured from the top to the bottom) across the
is the potential difference (measured from the top to the bottom) across the 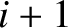 th capacitor (from the left) in the
circuit shown in Exercise 3, and
th capacitor (from the left) in the
circuit shown in Exercise 3, and 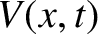 is the corresponding voltage in the transmission line, show that the discrete circuit equations relating the
is the corresponding voltage in the transmission line, show that the discrete circuit equations relating the 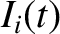 and
and 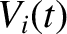 reduce to
reduce to
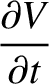 |
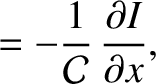 |
|
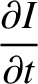 |
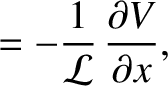 |
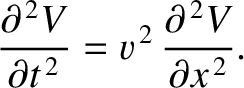
 , tension
, tension  , and mass per unit length
, and mass per unit length  that is stretched between two immovable walls.
that is stretched between two immovable walls.
![$\displaystyle E = \frac{1}{2}\int_0^l\left[\rho\left(\frac{\partial y}{\partial t}\right)^2
+ T\left(\frac{\partial y}{\partial x}\right)^2\right] dx,
$](img1111.png)
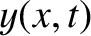 is the string's (relatively small) transverse displacement.
is the string's (relatively small) transverse displacement.
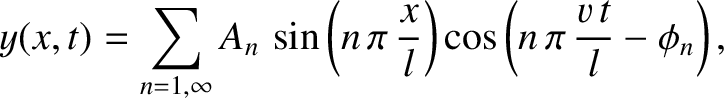
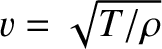 . Demonstrate that
. Demonstrate that
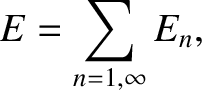

 th normal mode. Here,
th normal mode. Here,  is the mass of the
string, and
is the mass of the
string, and
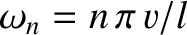 the angular frequency of the
the angular frequency of the  th normal
mode.
th normal
mode.