Next: Transverse Standing Waves Up: Coupled Oscillations Previous: Three Spring-Coupled Masses Contents
 is attached to a rigid support by means of a spring of
spring constant
is attached to a rigid support by means of a spring of
spring constant  . At equilibrium, the spring hangs vertically
downward. An identical oscillator is added to this system, the
spring of the former being attached to the mass of the latter.
Calculate the normal frequencies for one-dimensional vertical
oscillations about the equilibrium state, and describe the associated normal modes.
. At equilibrium, the spring hangs vertically
downward. An identical oscillator is added to this system, the
spring of the former being attached to the mass of the latter.
Calculate the normal frequencies for one-dimensional vertical
oscillations about the equilibrium state, and describe the associated normal modes.
 , the two outer springs have spring constant
, the two outer springs have spring constant
 , and the middle spring has spring constant
, and the middle spring has spring constant 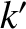 . Find the normal
frequencies and normal modes in terms of
. Find the normal
frequencies and normal modes in terms of
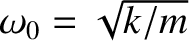 and
and
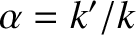 .
.
 , the two leftmost springs have spring constant
, the two leftmost springs have spring constant
 , and the rightmost spring is absent. Find the normal
frequencies and normal modes in terms of
, and the rightmost spring is absent. Find the normal
frequencies and normal modes in terms of
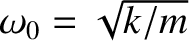 .
.
 , and the
left and right masses are of mass
, and the
left and right masses are of mass  and
and 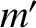 , respectively. Find the normal
frequencies and normal modes in terms of
, respectively. Find the normal
frequencies and normal modes in terms of
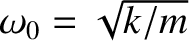 and
and
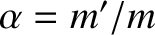 .
.
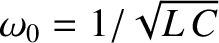 and
and
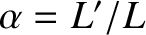 .
.
 , but different bob masses,
, but different bob masses, 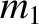 and
and 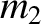 . Suppose
that the pendula are connected by a spring of spring constant
. Suppose
that the pendula are connected by a spring of spring constant  .
Let the spring be unextended when the two bobs are in their equilibrium
positions.
.
Let the spring be unextended when the two bobs are in their equilibrium
positions.
 |
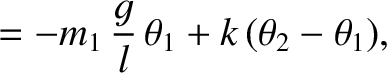 |
|
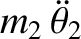 |
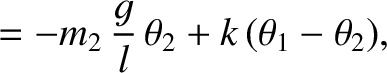 |
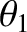 and
and 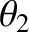 are the angular displacements of the respective
pendula from their equilibrium positions.
are the angular displacements of the respective
pendula from their equilibrium positions.
 and
and
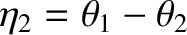 .
Find the normal frequencies.
.
Find the normal frequencies.
 the
two pendula are stationary, with
the
two pendula are stationary, with
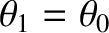 , and
, and
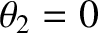 .
.
 and
and 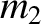 , slide over a horizontal frictionless surface, and are connected via a spring of
force constant
, slide over a horizontal frictionless surface, and are connected via a spring of
force constant  . Mass
. Mass 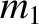 is acted on by a horizontal force
is acted on by a horizontal force
 . In the absence of the
second mass, this force causes the first mass to execute simple harmonic motion of amplitude
. In the absence of the
second mass, this force causes the first mass to execute simple harmonic motion of amplitude
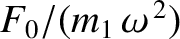 .
Find an appropriate choice of the combination of values
.
Find an appropriate choice of the combination of values 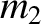 and
and  that reduces the oscillation amplitude of
that reduces the oscillation amplitude of 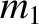 as much as possible. What is the oscillation amplitude of
as much as possible. What is the oscillation amplitude of 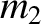 in this case?
in this case?
 flanked by two identical atoms of
mass
flanked by two identical atoms of
mass  . The atomic bonds are represented as springs of spring constant
. The atomic bonds are represented as springs of spring constant  .
Find the molecule's normal frequencies and modes of linear oscillation.
.
Find the molecule's normal frequencies and modes of linear oscillation.
![$\displaystyle E = m\left[\frac{1}{2}\left(\dot{x}_1^{\,2}+\dot{x}_2^{\,2}\right) + \omega_0^{\,2}\left(x_1^{\,2}-x_1\,x_2+x_2^{\,2}\right)\right].
$](img852.png)
![$\displaystyle E= m\left[\left(\dot{\eta}_1^{\,2}+\dot{\eta}_2^{\,2}\right) + \omega_0^{\,2}\left(\eta_1^{\,2}+3\,\eta_2^{\,2}\right)\right]
$](img853.png)
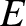 |
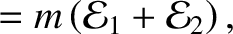 |
|
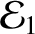 |
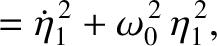 |
|
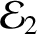 |
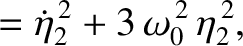 |
|
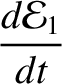 |
 |
|
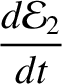 |
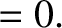 |
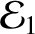 and
and
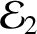 are the separately conserved energies per unit masses of the first and
second normal modes, respectively.
are the separately conserved energies per unit masses of the first and
second normal modes, respectively.