Next: General Solution of 1D Up: Wave Pulses Previous: Fourier Transforms Contents
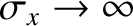 , or, equivalently,
, or, equivalently,
 . There is no difficulty in seeing, from Equation (8.15), that
. There is no difficulty in seeing, from Equation (8.15), that
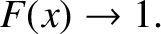 |
(8.21) |
 , Equation (8.16) yields a
, Equation (8.16) yields a  -space function that
is zero everywhere apart from
-space function that
is zero everywhere apart from 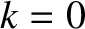 (because the function is negligible for
(because the function is negligible for
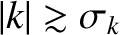 ), where it is infinite [because the function takes the value
), where it is infinite [because the function takes the value
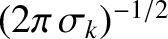 at
at 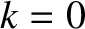 ]. Moreover, according to
Equation (8.20), the integral of the function over all
]. Moreover, according to
Equation (8.20), the integral of the function over all  remains unity. Thus, the
Fourier transform of the uniform function
remains unity. Thus, the
Fourier transform of the uniform function 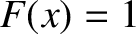 is a sort of integrable “spike”
located at
is a sort of integrable “spike”
located at 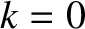 . This unusual function is known as the Dirac delta function, and
is denoted
. This unusual function is known as the Dirac delta function, and
is denoted
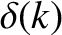 . Thus, one definition of a delta function is
. Thus, one definition of a delta function is
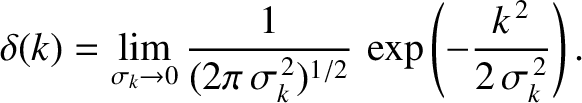 |
(8.22) |
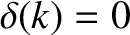 for
for 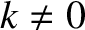 , and
, and
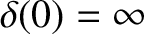 .
Moreover,
.
Moreover,
Consider the integral
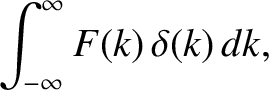 |
(8.24) |
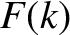 is an arbitrary function.
Because of the peculiar properties of the delta function, the only contribution
to the previous integral comes from the region in
is an arbitrary function.
Because of the peculiar properties of the delta function, the only contribution
to the previous integral comes from the region in  -space in the immediate vicinity of
-space in the immediate vicinity of 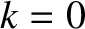 . Furthermore, provided
. Furthermore, provided 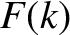 is well behaved in this region, we can write
is well behaved in this region, we can write
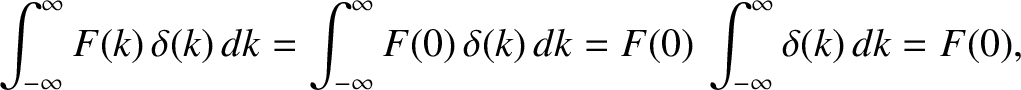 |
(8.25) |
A change of variables allows us to define
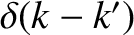 , which is a
“spike” function centered on
, which is a
“spike” function centered on 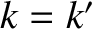 . The previous result can be generalized
to give
. The previous result can be generalized
to give
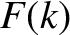 that are well behaved at
that are well behaved at 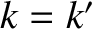 .
Indeed, this expression can be thought of as an alternative definition of a
delta function.
Incidentally, a Dirac delta function is sometimes referred to as a generalized function. This nomenclature arises because
the actual value of the function is ill defined (for instance, it would be impossible to graph the function),
whereas its integral is perfectly well defined (as evidenced by the previous equation).
.
Indeed, this expression can be thought of as an alternative definition of a
delta function.
Incidentally, a Dirac delta function is sometimes referred to as a generalized function. This nomenclature arises because
the actual value of the function is ill defined (for instance, it would be impossible to graph the function),
whereas its integral is perfectly well defined (as evidenced by the previous equation).
We have seen that the delta function 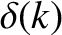 is the cosine Fourier transform of
the uniform function
is the cosine Fourier transform of
the uniform function 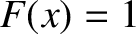 . It, thus, follows from Equation (8.11) that
. It, thus, follows from Equation (8.11) that
![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^\infty \cos(k\,x)\,\cos(k'\,x)\,dx
=...
...}^\infty\left\{\cos\left[(k-k')\,x\right]+\cos\left[(k+k')\,x\right]\right\}dx,$](img2393.png) |
(8.29) |