Consider a sinusoidal wave of angular frequency  and wavenumber
and wavenumber  that is propagating
in the
that is propagating
in the 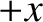 -direction. We can represent the wave in terms of a wavefunction of the form
-direction. We can represent the wave in terms of a wavefunction of the form
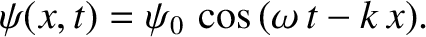 |
(6.153) |
The wavelength and frequency of the wave, as seen by a stationary observer, are
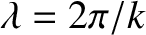 and
and
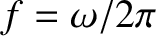 , respectively. Consider a second
observer moving with uniform speed
, respectively. Consider a second
observer moving with uniform speed 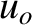 in the
in the 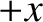 -direction. What are
the wavelength and frequency of the wave seen by the latter observer?
Assuming non-relativistic motion, the
-direction. What are
the wavelength and frequency of the wave seen by the latter observer?
Assuming non-relativistic motion, the  -coordinate in the moving observer's frame of reference
is given by the standard Gallilean transformation formula
-coordinate in the moving observer's frame of reference
is given by the standard Gallilean transformation formula
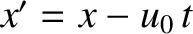 (Rindler 1997). Both observers measure
the same time. Hence, in the second observer's frame of reference, the
wavefunction is written
(Rindler 1997). Both observers measure
the same time. Hence, in the second observer's frame of reference, the
wavefunction is written
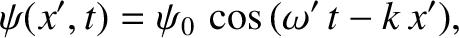 |
(6.154) |
where
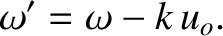 |
(6.155) |
Here, we have replaced  by
by 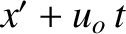 in Equation (6.153).
Thus, the moving observer sees a wave possessing the same wavelength (
i.e., the same
in Equation (6.153).
Thus, the moving observer sees a wave possessing the same wavelength (
i.e., the same  ) but a different frequency (i.e., a different
) but a different frequency (i.e., a different  )
to that seen by the stationary observer. This phenomenon is known as the Doppler effect.
If
)
to that seen by the stationary observer. This phenomenon is known as the Doppler effect.
If 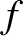 is the wave frequency (in hertz) seen by the stationary observer then
the wave frequency seen by
the moving observer is
is the wave frequency (in hertz) seen by the stationary observer then
the wave frequency seen by
the moving observer is
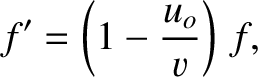 |
(6.156) |
where
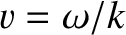 is the characteristic wave speed.
Thus, an observer moving in the same direction as a wave sees a lower frequency than a stationary observer. On the other hand, an observer moving in the opposite direction to a wave sees a higher frequency
than a stationary observer. Hence, the general Doppler shift formula (for a moving observer and
a stationary wave source) is
is the characteristic wave speed.
Thus, an observer moving in the same direction as a wave sees a lower frequency than a stationary observer. On the other hand, an observer moving in the opposite direction to a wave sees a higher frequency
than a stationary observer. Hence, the general Doppler shift formula (for a moving observer and
a stationary wave source) is
 |
(6.157) |
where the upper/lower signs correspond to the observer moving in the same/opposite direction
to the wave.
Consider a stationary observer measuring a wave emitted by a source that is moving towards
the observer with speed 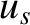 . Let
. Let 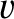 be the characteristic propagation speed of the wave.
Consider two neighboring wave crests emitted by the source. Suppose that the first is
emitted at time
be the characteristic propagation speed of the wave.
Consider two neighboring wave crests emitted by the source. Suppose that the first is
emitted at time  , and the second at time
, and the second at time 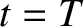 , where
, where 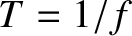 is the wave period in the
frame of reference of the source. At time
is the wave period in the
frame of reference of the source. At time  , the first wave crest has traveled a distance
, the first wave crest has traveled a distance
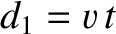 towards the observer, whereas the second wave crest has traveled a distance
towards the observer, whereas the second wave crest has traveled a distance
 (measured from the position of the
source at
(measured from the position of the
source at  ). Here, we have taken into account the fact that the source is
a distance
). Here, we have taken into account the fact that the source is
a distance 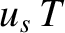 closer to the observer when the second wave crest is emitted.
The effective wavelength,
closer to the observer when the second wave crest is emitted.
The effective wavelength, 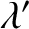 , seen by the observer is the distance between neighboring
wave crests. Hence,
, seen by the observer is the distance between neighboring
wave crests. Hence,
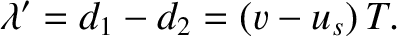 |
(6.158) |
Because
 ,
the effective frequency
,
the effective frequency 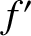 seen by the observer is
seen by the observer is
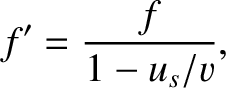 |
(6.159) |
where 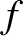 is the wave frequency in the frame of reference of the source. We conclude that if the
source is moving towards the observer then the wave frequency is shifted upwards. Likewise,
if the source is moving away from the observer then the frequency is shifted downwards.
This manifestation of the Doppler effect is familiar from everyday experience. When an ambulance
passes us on the street, its siren has a higher pitch (i.e., a high
frequency) when it is coming towards us than when it is moving away from us.
In fact, the oscillation frequency of the siren never changes. It is the Doppler
shift induced by the motion of the siren with respect to a stationary listener that
causes the frequency change.
is the wave frequency in the frame of reference of the source. We conclude that if the
source is moving towards the observer then the wave frequency is shifted upwards. Likewise,
if the source is moving away from the observer then the frequency is shifted downwards.
This manifestation of the Doppler effect is familiar from everyday experience. When an ambulance
passes us on the street, its siren has a higher pitch (i.e., a high
frequency) when it is coming towards us than when it is moving away from us.
In fact, the oscillation frequency of the siren never changes. It is the Doppler
shift induced by the motion of the siren with respect to a stationary listener that
causes the frequency change.
The general formula for the shift in wave frequency induced by
relative motion of an observer and a source is
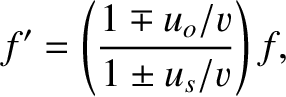 |
(6.160) |
where 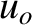 is the speed of the observer, and
is the speed of the observer, and 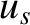 is the speed of the source (both measured relative to the wave medium).
The upper/lower signs correspond to relative motion by which the observer and the source
move apart/together. If the observer and source are not moving directly toward or directly away from
one another then the quantities
is the speed of the source (both measured relative to the wave medium).
The upper/lower signs correspond to relative motion by which the observer and the source
move apart/together. If the observer and source are not moving directly toward or directly away from
one another then the quantities 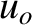 and
and 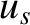 in the above formulae correspond to the components of the observer and source velocities, respectively,
along the straight line that instantaneously joins them.
in the above formulae correspond to the components of the observer and source velocities, respectively,
along the straight line that instantaneously joins them.
An important proviso to the previous formula is that it is strictly classical, and only holds for non-relativistic motion (i.e., 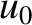 ,
, 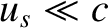 , where
, where
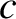 is the velocity of light in vacuum.) In fact, when applied to light propagation in a vacuum, the formula is only accurate up to first-order
in
is the velocity of light in vacuum.) In fact, when applied to light propagation in a vacuum, the formula is only accurate up to first-order
in 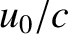 and
and 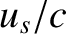 (Rindler 1997). In other words, for light propagation the previous equation reduces to
(Rindler 1997). In other words, for light propagation the previous equation reduces to
![$\displaystyle f'=\left[1-\frac{u}{c}+{\cal O}\left(\frac{u^{\,2}}{c^{\,2}}\right)\right]f,$](img1718.png) |
(6.161) |
where 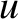 is the relative radial velocity of the source with respect to the observer (being positive when the source and observer are
moving apart, and vice versa).
is the relative radial velocity of the source with respect to the observer (being positive when the source and observer are
moving apart, and vice versa).
Probably the most well-known use of the Doppler effect in everyday life is in police speed
traps. In such a trap, a police officer fires radar waves (i.e., electromagnetic
waves of centimeter wavelength) of fixed frequency at an oncoming car. These waves
reflect off the car, which effectively becomes a moving source. Hence, by measuring the frequency increase
of the reflected waves, the officer can determine the car's speed.
 and wavenumber
and wavenumber  that is propagating
in the
that is propagating
in the 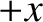 -direction. We can represent the wave in terms of a wavefunction of the form
The wavelength and frequency of the wave, as seen by a stationary observer, are
-direction. We can represent the wave in terms of a wavefunction of the form
The wavelength and frequency of the wave, as seen by a stationary observer, are
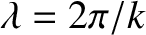 and
and
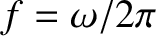 , respectively. Consider a second
observer moving with uniform speed
, respectively. Consider a second
observer moving with uniform speed 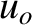 in the
in the 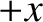 -direction. What are
the wavelength and frequency of the wave seen by the latter observer?
Assuming non-relativistic motion, the
-direction. What are
the wavelength and frequency of the wave seen by the latter observer?
Assuming non-relativistic motion, the  -coordinate in the moving observer's frame of reference
is given by the standard Gallilean transformation formula
-coordinate in the moving observer's frame of reference
is given by the standard Gallilean transformation formula
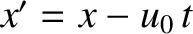 (Rindler 1997). Both observers measure
the same time. Hence, in the second observer's frame of reference, the
wavefunction is written
(Rindler 1997). Both observers measure
the same time. Hence, in the second observer's frame of reference, the
wavefunction is written
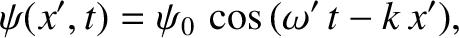
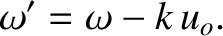
 by
by 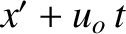 in Equation (6.153).
Thus, the moving observer sees a wave possessing the same wavelength (
i.e., the same
in Equation (6.153).
Thus, the moving observer sees a wave possessing the same wavelength (
i.e., the same  ) but a different frequency (i.e., a different
) but a different frequency (i.e., a different  )
to that seen by the stationary observer. This phenomenon is known as the Doppler effect.
If
)
to that seen by the stationary observer. This phenomenon is known as the Doppler effect.
If 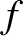 is the wave frequency (in hertz) seen by the stationary observer then
the wave frequency seen by
the moving observer is
is the wave frequency (in hertz) seen by the stationary observer then
the wave frequency seen by
the moving observer is
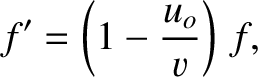
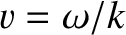 is the characteristic wave speed.
Thus, an observer moving in the same direction as a wave sees a lower frequency than a stationary observer. On the other hand, an observer moving in the opposite direction to a wave sees a higher frequency
than a stationary observer. Hence, the general Doppler shift formula (for a moving observer and
a stationary wave source) is
is the characteristic wave speed.
Thus, an observer moving in the same direction as a wave sees a lower frequency than a stationary observer. On the other hand, an observer moving in the opposite direction to a wave sees a higher frequency
than a stationary observer. Hence, the general Doppler shift formula (for a moving observer and
a stationary wave source) is

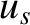 . Let
. Let 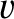 be the characteristic propagation speed of the wave.
Consider two neighboring wave crests emitted by the source. Suppose that the first is
emitted at time
be the characteristic propagation speed of the wave.
Consider two neighboring wave crests emitted by the source. Suppose that the first is
emitted at time  , and the second at time
, and the second at time 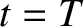 , where
, where 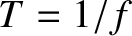 is the wave period in the
frame of reference of the source. At time
is the wave period in the
frame of reference of the source. At time  , the first wave crest has traveled a distance
, the first wave crest has traveled a distance
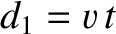 towards the observer, whereas the second wave crest has traveled a distance
towards the observer, whereas the second wave crest has traveled a distance
 (measured from the position of the
source at
(measured from the position of the
source at  ). Here, we have taken into account the fact that the source is
a distance
). Here, we have taken into account the fact that the source is
a distance 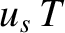 closer to the observer when the second wave crest is emitted.
The effective wavelength,
closer to the observer when the second wave crest is emitted.
The effective wavelength, 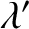 , seen by the observer is the distance between neighboring
wave crests. Hence,
, seen by the observer is the distance between neighboring
wave crests. Hence,
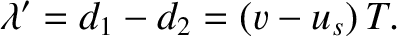
 ,
the effective frequency
,
the effective frequency 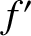 seen by the observer is
seen by the observer is
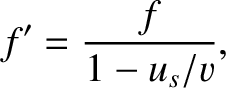
 is the wave frequency in the frame of reference of the source. We conclude that if the
source is moving towards the observer then the wave frequency is shifted upwards. Likewise,
if the source is moving away from the observer then the frequency is shifted downwards.
This manifestation of the Doppler effect is familiar from everyday experience. When an ambulance
passes us on the street, its siren has a higher pitch (i.e., a high
frequency) when it is coming towards us than when it is moving away from us.
In fact, the oscillation frequency of the siren never changes. It is the Doppler
shift induced by the motion of the siren with respect to a stationary listener that
causes the frequency change.
is the wave frequency in the frame of reference of the source. We conclude that if the
source is moving towards the observer then the wave frequency is shifted upwards. Likewise,
if the source is moving away from the observer then the frequency is shifted downwards.
This manifestation of the Doppler effect is familiar from everyday experience. When an ambulance
passes us on the street, its siren has a higher pitch (i.e., a high
frequency) when it is coming towards us than when it is moving away from us.
In fact, the oscillation frequency of the siren never changes. It is the Doppler
shift induced by the motion of the siren with respect to a stationary listener that
causes the frequency change.
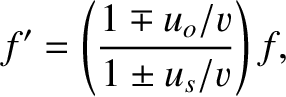
 is the speed of the observer, and
is the speed of the observer, and 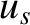 is the speed of the source (both measured relative to the wave medium).
The upper/lower signs correspond to relative motion by which the observer and the source
move apart/together. If the observer and source are not moving directly toward or directly away from
one another then the quantities
is the speed of the source (both measured relative to the wave medium).
The upper/lower signs correspond to relative motion by which the observer and the source
move apart/together. If the observer and source are not moving directly toward or directly away from
one another then the quantities 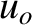 and
and 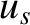 in the above formulae correspond to the components of the observer and source velocities, respectively,
along the straight line that instantaneously joins them.
in the above formulae correspond to the components of the observer and source velocities, respectively,
along the straight line that instantaneously joins them.
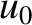 ,
, 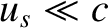 , where
, where
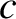 is the velocity of light in vacuum.) In fact, when applied to light propagation in a vacuum, the formula is only accurate up to first-order
in
is the velocity of light in vacuum.) In fact, when applied to light propagation in a vacuum, the formula is only accurate up to first-order
in 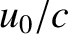 and
and 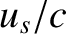 (Rindler 1997). In other words, for light propagation the previous equation reduces to
(Rindler 1997). In other words, for light propagation the previous equation reduces to
![$\displaystyle f'=\left[1-\frac{u}{c}+{\cal O}\left(\frac{u^{\,2}}{c^{\,2}}\right)\right]f,$](img1718.png)
 is the relative radial velocity of the source with respect to the observer (being positive when the source and observer are
moving apart, and vice versa).
is the relative radial velocity of the source with respect to the observer (being positive when the source and observer are
moving apart, and vice versa).