Two Coupled LC Circuits
Consider the LC circuit pictured in Figure 3.4. Let 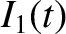 ,
, 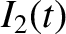 ,
and
,
and 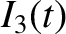 be the currents flowing in the three legs of the circuit, which meet
at junctions
be the currents flowing in the three legs of the circuit, which meet
at junctions  and
and 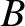 .
According to
Kirchhoff's first circuital law, the net current flowing into
each junction is zero (Grant and Phillips 1975). It follows that
.
According to
Kirchhoff's first circuital law, the net current flowing into
each junction is zero (Grant and Phillips 1975). It follows that
 . We deduce that this
is a two-degree-of-freedom system whose instantaneous configuration is
specified by the two independent variables
. We deduce that this
is a two-degree-of-freedom system whose instantaneous configuration is
specified by the two independent variables 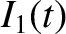 and
and 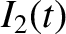 . It follows that there
are two independent normal modes of oscillation.
The potential drops across the left, middle, and right legs of the circuit are
. It follows that there
are two independent normal modes of oscillation.
The potential drops across the left, middle, and right legs of the circuit are
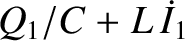 ,
, 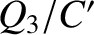 , and
, and
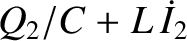 ,
respectively, where
,
respectively, where
 ,
,
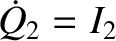 , and
, and
 .
However, because the
three legs are connected in parallel with one another, the potential drops must
all be equal, so that
Differentiating with respect to
.
However, because the
three legs are connected in parallel with one another, the potential drops must
all be equal, so that
Differentiating with respect to  , dividing by
, dividing by 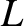 , and rearranging, we obtain the coupled time evolution
equations of the system:
where
, and rearranging, we obtain the coupled time evolution
equations of the system:
where
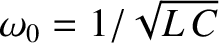 and
and
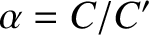 .
.
Figure 3.4:
A two-degree-of-freedom LC circuit.
|
|
We can solve the problem in a systematic manner by
searching for a normal mode of the form
Substitution into the time evolution equations (3.36) and (3.37)
yields the homogeneous matrix equation
![\begin{displaymath}\left(
\begin{array}{cc}
\hat{\omega}^{\,2}-(1+\alpha), & -\a...
...ht) = \left(
\begin{array}{c}
0\\ [0.5ex] 0
\end{array}\right),\end{displaymath}](img758.png) |
(3.40) |
where
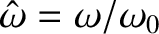 . The normal frequencies are
determined by setting the determinant of the matrix to zero. This gives
. The normal frequencies are
determined by setting the determinant of the matrix to zero. This gives
![$\displaystyle \left[\hat{\omega}^{\,2}-(1+\alpha)\right]^{\,2}-\alpha^{\,2} = 0,$](img759.png) |
(3.41) |
or
![$\displaystyle \hat{\omega}^{\,4} - 2\,(1+\alpha)\,\hat{\omega}^{\,2}+1+2\,\alph...
...eft(\hat{\omega}^{\,2}-1\right)\left(\hat{\omega}^{\,2}-[1+2\,\alpha]\right)=0.$](img760.png) |
(3.42) |
The roots of the preceding equation
are
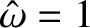 and
and
 . (Again, we have neglected the
negative frequency roots, because they generate the same patterns of motion as the
corresponding positive frequency roots.)
Hence, the two
normal frequencies are
. (Again, we have neglected the
negative frequency roots, because they generate the same patterns of motion as the
corresponding positive frequency roots.)
Hence, the two
normal frequencies are 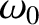 and
and
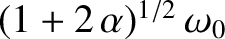 .
The characteristic patterns of motion associated with the normal modes
can be calculated from the first row of the matrix equation (3.40),
which can be rearranged to give
.
The characteristic patterns of motion associated with the normal modes
can be calculated from the first row of the matrix equation (3.40),
which can be rearranged to give
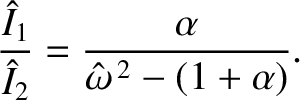 |
(3.43) |
It follows that
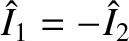 for the normal mode with
for the normal mode with
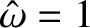 ,
and
,
and
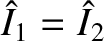 for the normal mode with
for the normal mode with
 . The most general solution, thus, takes the form
where
. The most general solution, thus, takes the form
where
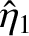 and
and  are the amplitude and phase of the higher frequency
normal mode, whereas
are the amplitude and phase of the higher frequency
normal mode, whereas
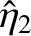 and
and 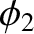 are the amplitude and phase of the lower frequency
mode.
are the amplitude and phase of the lower frequency
mode.
Figure: 3.5
Time evolution of the physical coordinates of the two-degree-of-freedom LC circuit pictured in Figure 3.4.
The initial conditions are
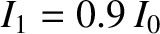 ,
,
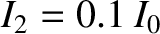 ,
,
 .
The solid curve
corresponds to
.
The solid curve
corresponds to 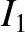 , and the dashed curve to
, and the dashed curve to 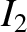 . Here,
. Here,
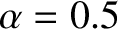 , and
, and
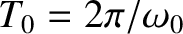 .
.
|
|
It is fairly easy to guess that the normal coordinates of the system are
Forming the sum and difference of Equations (3.36)
and (3.37), we obtain the evolution equations for the two
independent normal modes of oscillation,
(We can be sure that we have correctly guessed the normal coordinates because the previous two equations do
not couple to one another.)
These equations can readily be solved to give
where
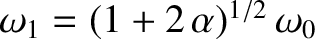 . Here,
. Here,
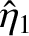 ,
,  ,
,
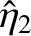 , and
, and 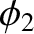 are
arbitrary constants. Note that the previous two equations, when combined with Equations (3.46) and (3.47) (which imply that
are
arbitrary constants. Note that the previous two equations, when combined with Equations (3.46) and (3.47) (which imply that
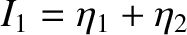 and
and
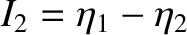 ), are equivalent to our previous solution, (3.44) and (3.45).
), are equivalent to our previous solution, (3.44) and (3.45).
As an example, suppose that
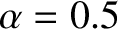 . Furthermore, let
. Furthermore, let
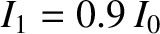 ,
,
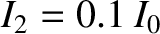 , and
, and
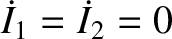 , at
, at  ,
where
,
where  is an arbitrary constant. The time evolution of the system is illustrated in Figures 3.5 and 3.6. Note that the
normal coordinates oscillate sinusoidally, whereas the time evolution of the physical coordinates is
more complicated.
is an arbitrary constant. The time evolution of the system is illustrated in Figures 3.5 and 3.6. Note that the
normal coordinates oscillate sinusoidally, whereas the time evolution of the physical coordinates is
more complicated.
Figure: 3.6
Time evolution of the normal coordinates of the two-degree-of-freedom LC circuit pictured in Figure 3.4.
The initial conditions are
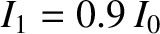 ,
,
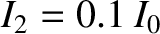 ,
,
 .
The solid curve
corresponds to
.
The solid curve
corresponds to 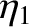 , and the dashed curve to
, and the dashed curve to 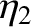 . Here,
. Here,
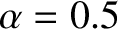 , and
, and
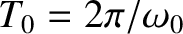 .
.
|
|
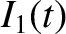 ,
, 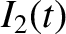 ,
and
,
and 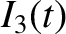 be the currents flowing in the three legs of the circuit, which meet
at junctions
be the currents flowing in the three legs of the circuit, which meet
at junctions  and
and 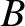 .
According to
Kirchhoff's first circuital law, the net current flowing into
each junction is zero (Grant and Phillips 1975). It follows that
.
According to
Kirchhoff's first circuital law, the net current flowing into
each junction is zero (Grant and Phillips 1975). It follows that
 . We deduce that this
is a two-degree-of-freedom system whose instantaneous configuration is
specified by the two independent variables
. We deduce that this
is a two-degree-of-freedom system whose instantaneous configuration is
specified by the two independent variables 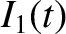 and
and 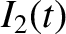 . It follows that there
are two independent normal modes of oscillation.
The potential drops across the left, middle, and right legs of the circuit are
. It follows that there
are two independent normal modes of oscillation.
The potential drops across the left, middle, and right legs of the circuit are
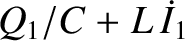 ,
, 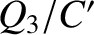 , and
, and
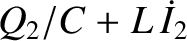 ,
respectively, where
,
respectively, where
 ,
,
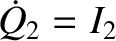 , and
, and
 .
However, because the
three legs are connected in parallel with one another, the potential drops must
all be equal, so that
.
However, because the
three legs are connected in parallel with one another, the potential drops must
all be equal, so that
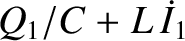
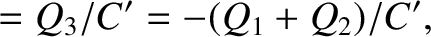
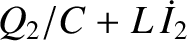
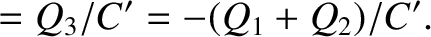
 , dividing by
, dividing by 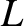 , and rearranging, we obtain the coupled time evolution
equations of the system:
where
, and rearranging, we obtain the coupled time evolution
equations of the system:
where
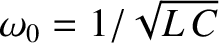 and
and
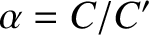 .
.

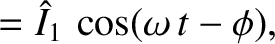

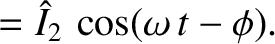
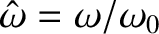 . The normal frequencies are
determined by setting the determinant of the matrix to zero. This gives
. The normal frequencies are
determined by setting the determinant of the matrix to zero. This gives
![$\displaystyle \left[\hat{\omega}^{\,2}-(1+\alpha)\right]^{\,2}-\alpha^{\,2} = 0,$](img759.png)
![$\displaystyle \hat{\omega}^{\,4} - 2\,(1+\alpha)\,\hat{\omega}^{\,2}+1+2\,\alph...
...eft(\hat{\omega}^{\,2}-1\right)\left(\hat{\omega}^{\,2}-[1+2\,\alpha]\right)=0.$](img760.png)
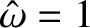 and
and
 . (Again, we have neglected the
negative frequency roots, because they generate the same patterns of motion as the
corresponding positive frequency roots.)
Hence, the two
normal frequencies are
. (Again, we have neglected the
negative frequency roots, because they generate the same patterns of motion as the
corresponding positive frequency roots.)
Hence, the two
normal frequencies are 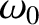 and
and
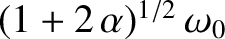 .
The characteristic patterns of motion associated with the normal modes
can be calculated from the first row of the matrix equation (3.40),
which can be rearranged to give
.
The characteristic patterns of motion associated with the normal modes
can be calculated from the first row of the matrix equation (3.40),
which can be rearranged to give
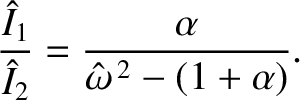
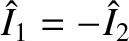 for the normal mode with
for the normal mode with
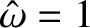 ,
and
,
and
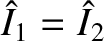 for the normal mode with
for the normal mode with
 . The most general solution, thus, takes the form
where
. The most general solution, thus, takes the form
where
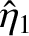 and
and  are the amplitude and phase of the higher frequency
normal mode, whereas
are the amplitude and phase of the higher frequency
normal mode, whereas
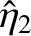 and
and 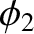 are the amplitude and phase of the lower frequency
mode.
are the amplitude and phase of the lower frequency
mode.
![\includegraphics[width=0.8\textwidth]{Chapter03/fig3_05.eps}](img768.png)
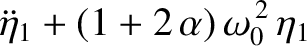
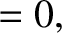
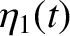
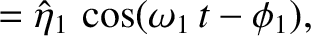

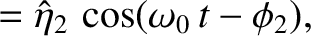
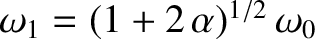 . Here,
. Here,
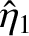 ,
,  ,
,
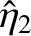 , and
, and 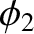 are
arbitrary constants. Note that the previous two equations, when combined with Equations (3.46) and (3.47) (which imply that
are
arbitrary constants. Note that the previous two equations, when combined with Equations (3.46) and (3.47) (which imply that
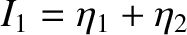 and
and
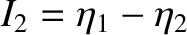 ), are equivalent to our previous solution, (3.44) and (3.45).
), are equivalent to our previous solution, (3.44) and (3.45).
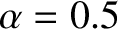 . Furthermore, let
. Furthermore, let
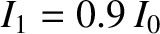 ,
,
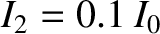 , and
, and
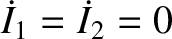 , at
, at  ,
where
,
where  is an arbitrary constant. The time evolution of the system is illustrated in Figures 3.5 and 3.6. Note that the
normal coordinates oscillate sinusoidally, whereas the time evolution of the physical coordinates is
more complicated.
is an arbitrary constant. The time evolution of the system is illustrated in Figures 3.5 and 3.6. Note that the
normal coordinates oscillate sinusoidally, whereas the time evolution of the physical coordinates is
more complicated.
![\includegraphics[width=0.8\textwidth]{Chapter03/fig3_06.eps}](img784.png)